Living Systems Theory – LST Basics
James Grier Miller
Living Systems – The Basic Concepts
(1978)
https://en.wikipedia.org/wiki/Living_systems
https://en.wikipedia.org/wiki/Systems_theory
Note
This is a complex beautiful text that should be read by all those who intend to put the so-called social sciences on a truly scientific basis in order to reach a unification of knowledge, at least as far as methodology is concerned.
As stated by the author: “If the social sciences were to formulate their problems, whenever possible, in the way which has proved most convenient for the natural sciences over centuries, unification of all the sciences would be accelerated.” And this is a very urgent task if we want to get out of the obscurantist nonsense that still characterizes much of social analysis and social remedies.
General systems theory is a set of related definitions, assumptions, and propositions which deal with reality as an integrated hierarchy of organizations of matter and energy. General living systems theory is concerned with a special subset of all systems, the living ones. Even more basic to this presentation than the concept of “system” are the concepts of “space,” “time,” “matter,” “energy,” and “information,” because the living systems which I shall discuss exist in space and are made of matter and energy organized by information.
1. Space and time
In the most general mathematical sense, a space is a set of elements which conform to certain postulates. Euclidean space, for instance, consists of points in three dimensions which are subject to the postulates of Euclid. In a metric space a distance measure is associated with each pair of elements. In a topological space each element has a collection of neighborhoods. The conceptual spaces of mathematics may have any number of dimensions.
Physical space is the extension surrounding a point. It may be thought of as either the compass of the entire universe or some region of such a universe. Classically the three-dimensional geometry of Euclid was considered to describe accurately all regions in physical space. The modern general theory of relativity has shown that physical space-time is more accurately described by a Riemannian geometry of four non-uniformly curved dimensions, three of space and one of time.
My presentation of a general theory of living systems will employ two sorts of spaces in which they may exist, physical or geographical space and conceptual or abstracted spaces.
1.1 Physical or geographical space
This will be considered as Euclidean space, which is adequate for the study of all aspects of living systems as we now know them. Among the characteristics and constraints of physical space are the following: (a) The distance from point A to point B is the same as that from point B to point A. (b) Matter or energy moving on a straight or curved path from point A to point B must pass through every intervening point on the path. This is true also of markers bearing information. (c) In such space there is a maximum speed of movement for matter, energy, and markers bearing information. (d) Objects in such space exert gravitational pull on each other. (e) Solid objects moving in such space cannot pass through one another. (f) Solid objects moving in such space are subject to friction when they contact another object.
The characteristics and constraints of physical space affect the action of all concrete systems, living and nonliving. The following are some examples: (a) The number of different nucleotide bases-configurations in space-which a DNA molecule has determines how many bits of information it can store. (b) On the average, people interact more with persons who live near to them in a housing project than with persons who live far away in the project. (c) The diameter of the fuel supply lines laid down behind General Patton’s advancing American Third Army in World War II determined the amount of friction the lines exerted upon the fuel pumped through them, and therefore the rate at which fuel could flow through them to supply Patton’s tanks. This was one physical constraint which limited the rate at which the army could advance, because they had to halt when they ran out of fuel. (d) The small physical size of Goa in relation to India and its spatial contiguity to India were, in 1961, major determinants in the decision of erstwhile neutralist India to invade and seize it. (e) Today information can flow worldwide almost instantly by telegraph, radio, and television. In the seventeenth century it took weeks for messages to cross an ocean. A government could not send messages to its ambassadors so quickly then as it can now because of the constraints on the rate of movement of the marker bearing the information. Consequently ambassadors of that century had much more freedom of decision than they do now.
Physical space is a common space because it is the only space in which all concrete systems, living and nonliving, exist (though some may exist in other spaces simultaneously). Physical space is shared by all scientific observers, and all scientific data must be collected in it. This is equally true for natural science and behavioral science.
Most people learn that physical space exists, which is not true of many spaces I shall mention in the next section. They can give the location of objects in it. A child probably learns of physical space by correlating the spaces presented by at least two sense modalities – such as vision (which may be distorted by such pathologies as astigmatism or aniseikonia), touch, or hearing (which may be distorted by partial or unilateral deafness). Physical space as experienced by an individual is that space which has the greatest commonality with the spaces presented by all his sense modalities.
1.2 Conceptual or abstracted spaces
Scientific observers often view living systems as existing in spaces which they conceptualize or abstract from the phenomena with which they deal. Examples of such spaces are: (a) Peck order in birds or other animals. (b) Social class space, in which Warner locates six social classes (lower lower, upper lower, lower middle, upper middle, lower upper, and upper upper classes). (c) Social distance among ethnic or racial groups. (d) Political distance among political parties of the Right and the Left. (e) The life space of Lewin, environment as seen by the subject, including the field forces or valences between him and objects in the environment, which can account for his immediately subsequent behavior. (f) Osgood’s semantic space as determined by subjects’ ratings of words on the semantic differential test. (g) Sociometric space, e.g., the rating on a scale of leadership ability of each member of a group by every other member. (h) A space of time costs of various modes of transportation, e.g., travel taking longer on foot than by air, longer upstream than down. (i) A space representing the shortest distances for messages to travel among various points on a telephone network. These may not be the same as the distances among those points in physical space. (j) A space of frequency of trade relations among nations. (k) A space of frequency of intermarriage among ethnic groups.
These conceptual and abstracted spaces do not have the same characteristics and are not subject to the same constraints as physical space. Each has characteristics and constraints of its own. These spaces may be either conceived of by a human being or learned about from others. Interpreting the meaning of such spaces, observing relations, and measuring distances in them ordinarily require human observers. Consequently the biases of individual human beings color these observations. Perhaps pattern-recognition computer programs can someday be written to make such observations with more objective precision.
Social and some biological scientists find conceptual or abstracted spaces useful because they recognize that physical space is not a major determinant of certain processes in the living systems they study. For example, no matter where they enter the body, most of the iodine atoms in the body accumulate in the thyroid gland. The most frequent interpersonal relations occur among persons of like interests or like attitudes rather than among geographical neighbors. Families frequently come together for holidays no matter how far apart their members are. Allies like England and Australia are often more distant from each other in physical space than they are from their enemies.
Scientists who make observations and measurements in any space other than physical space should attempt to indicate precisely what the transformations are from their space to physical space. Other spaces are definitely useful to science, but physical space is the only common space in which all concrete systems exist. A scientist who makes observations and measurements in another space, which he or someone else has conceptualized, is developing a special theory. At the same time, however, he is fractionating science unless he or someone else makes an effort to indicate the relationship of the space he is working in to physical space or to some other conceptual or abstracted spaces. Any transformation of one space to another is worth carrying out, and science will not be complete and unitary until transformations can be made from any given space to any other. One can, of course, conceive of spaces that cannot be transformed to other spaces, but it seems unlikely that they will apply to systems in physical space.
Not knowing at the moment how to carry out the transformation from the space one is making observations in to another space does not prevent one from conducting profitable studies. Many useful observations about heat were made in the space of degrees of temperature before the transformation from that space to the other spaces of the centimeter-gram-second system were known.
Any scientific observations about a designated space which cannot be transformed to other spaces concern a special theory. A general theory such as I shall develop here, however, requires that observations be made in a common space or in different spaces with known transformations. This is essential because one cannot measure comparable processes at different levels of systems, to confirm or disconfirm cross-level hypotheses, unless one can measure different levels of systems or dimensions in the same spaces or in different spaces with known transformations among them (see Sections 2 and 3 below). It must be possible, moreover, to make such measurements precisely enough to demonstrate whether or not there is a formal identity across levels.
1.3 Time.
This is the fundamental “fourth dimension” of the physical space-time continuum. Time is the particular instant at which a structure exists or a process occurs, or the measured or measurable period over which a structure endures or a process continues. For the study of all aspects of living systems as we now know them, for the measurement of durations, speeds, rates, and accelerations, the usual absolute scales of time – seconds, minutes, days, years – are adequate. The modern general theory of relativity, however, makes it clear that, particularly in the very large systems studied in astronomy, time cannot be accurately measured on any absolute scale of succession of events. Its measurement differs with the special reference frame of each particular observer, who has his own particular “clock.” A concrete system can move in any direction on the spatial dimensions, but only forward – never backward – on the temporal dimension. The irreversible unidirectionality of time is related to the second law of thermodynamics; a system tends to increase in entropy over time. Without new inputs higher in negentropy to the system, this process cannot be reversed in that system, and such inputs always increase the entropy outside the system. This principle has often been referred to as “time’s arrow.” It points only one way.
2. Matter and energy
Matter is anything which has mass (m) and occupies physical space. Energy (E) is defined in physics as the ability to do work. The principle of the conservation of energy states that energy can be neither created nor destroyed in the universe, but it may be converted from one form to another, including the energy equivalent of rest mass. Matter may have (a) kinetic energy, when it is moving and exerts a force on other matter; (b) potential energy, because of its position in a gravitational field; or (c) rest mass energy, which is the energy that would be released if mass were converted into energy. Mass and energy are equivalent. One can be converted into the other in accordance with the relation that rest mass energy is equal to the mass times the square of the velocity of light. Because of the known relationship between matter and energy, throughout this chapter I use the joint term matter-energy except where one or the other is specifically intended. Living systems need specific types of matter-energy in adequate amounts. Heat, light, water, minerals, vitamins, foods, fuels, and raw materials of various kinds, for instance, may be required. Energy for the processes of living systems is derived from the breakdown of molecules (and, in a few recent cases in social systems, of atoms as well). Any change of state of matter-energy or its movement over space, from one point to another, I shall call action. It is one form of process. (The term “action” is here used as in biology and behavioral science rather than as in physics.)
3. Information
Throughout this presentation information (H) will be used in the technical sense first suggested by Hartley in 1928 [Transmission of Information], and later developed by Shannon in his mathematical theory of communication [A Mathematical Theory of Communication]. It is not the same thing as meaning or quite the same as information as we usually understand it. Meaning is the significance of information to a system which processes it: it constitutes a change in that system’s processes elicited by the information, often resulting from associations made to it on previous experience with it. Information is a simpler concept: the degrees of freedom that exist in a given situation to choose among signals, symbols, messages, or patterns to be transmitted. The set of all these possible categories (the alphabet) is called the ensemble or repertoire. The amount of information is measured as the logarithm to the base 2 of the number of alternate patterns, forms, organizations, or messages. (When mX = y, then x is referred to as the logarithm of y to the base m.) The unit is the binary digit, or bit of information. It is the amount of information which relieves the uncertainty when the outcome of a situation with two equally likely alternatives is known. Legend says the American Revolution was begun by a signal to Paul Revere from Old North Church steeple. It could have been either one or two lights “one if by land or two if by sea.” If the alternatives were equally probable, the signal conveyed only one bit of information, resolving the uncertainty in a binary choice. But it carried a vast amount of meaning, meaning which must be measured by other sorts of units than bits. Signals convey information to the receiving system only if they do not duplicate information already in the receiver. As Gabor says:
Incomplete knowledge of the future, and also of the past of the transmitter from which the future might be constructed, is at the very basis of the concept of information. On the other hand, complete ignorance also precludes communication; a common language is required, that is to say an agreement between the transmitter and the receiver regarding the elements used in the communication process. . . . [The information of a message can] be defined as the ‘minimum number of binary decisions which enable the receiver to construct the message, on the basis of the data already available to him.’ These data comprise both the convention regarding the symbols and the language used, and the knowledge available at the moment when the message started. [A Summary of Communication Theory]
In many ways it is less useful to measure the amount of information than the amount of meaning. In later chapters, however, I reluctantly deal more with measurement of the amount of information than of meaning because as yet meaning cannot be precisely measured. Development of a rigorous and objective method for quantifying meaning would be a major contribution to the science of living systems.
Information is the negative of uncertainty. It is not accidental that the word “form” appears in “information,” since information is the amount of formal patterning or complexity in any system. Information theory is a set of concepts, theorems, and measures that were first developed by Shannon for communication engineering and have been extended to other, quite different fields, including theory of organization and theory of music. When all the assumptions about the situation and all its parameters are precisely stated, the amount of information can be rigorously measured in the structure and process of all sorts of living systems greatly different though they are.
The term marker was used by von Neumann to refer to those observable bundles, units, or changes of matter-energy whose patterning bears or conveys the informational symbols from the ensemble or repertoire. These might be the stones of Hammurabi’s day which bore cuneiform writing, parchments, writing paper, Indians’ smoke signals, a door key with notches, punched cards, paper or magnetic tape, a computer’s magnetized ferrite core memory, an arrangement of nucleotides in a DNA molecule, the molecular structure of a hormone, pulses on a telegraph wire, or waves emanating from a radio station. If a marker can assume n different states of which only one is present at any given time, it can represent at most log2n bits of information. The marker may be static, as in a book or in a computer’s memory. Communication of almost every sort requires that the marker move in space, from the transmitting system to the receiving system, and this movement follows the same physical laws as the movement of any other sort of matter-energy. The advance of communication technology over the years has been in the direction of decreasing the matter-energy costs of storing and transmitting the markers which bear information. The efficiency of information processing can be increased by lessening the mass of the markers, making them smaller so they can be stored more compactly and transmitted more rapidly and cheaply. Over the centuries engineering progress has altered the mode in markers from stones bearing cuneiform to magnetic tape bearing electrons, and clearly some limit is being approached. Cuneiform tablets carried approximately of the order of 10-2 bits of information per gram; paper with typewritten messages carries approximately of the order of 103 bits of information per gram; electronic magnetic tape storage carries approximately of the order of 106 bits of information per gram; and it has been demonstrated that one can write with micro-beams, through a demagnifying electron microscope on ultrafine grain films of silver halide in letters so small that they could store the content of more than a million books on a few cubic centimeters of tape, about 1012 bits per gram.
The mass of the matter-energy which makes up a system’s markers significantly affects its information processing. On the basis of quantum-mechanical considerations, Bremermann has estimated the minimum amount of energy that can serve as a marker. [Optimization through evolution and recombination] On the basis of this estimate he concluded that no system, living or nonliving, can process information at a rate greater than 2 x 1047 bits per second per gram of its mass. Suppose that the age of the earth is about 109 or 1010 years and its mass is less than 6 x 1027 g. A system the size of the earth, then, could process no more than 1093 bits of information in a period equal to the age of the earth. This is true even if the whole system is devoted to processing information, which never happens. It becomes clear that the minimum possible size of a marker is an important constraint on the capacity of living systems when one considers Minsky’s demonstration that the number of all possible sequences of moves in a single chess game is about 10120 Thus no earthly system, living or nonliving, could exhaustively review this many alternatives in playing a game. The human retina certainly can see more than a matrix of 100 x 100 spots, yet a matrix of this size can form 103000 possible patterns. There are, therefore, important practical matter-energy constraints upon the information processing of all living systems exerted by the nature of the matter-energy which composes their markers.
According to Quastler, information measures can be used to evaluate any kind of organization, since organization is based upon the interrelations among parts. [Information Theory Terms and Their Psychological Correlates] If two parts are interrelated either quantitatively or qualitatively, knowledge of the state of one must yield some information about the state of the other. Information measures can demonstrate when such relationships exist.
The antecedents of the information concepts include the early work related to thermodynamics of Maxwell, Planck, Boltzmann and Nabl, Helmholtz, and Gibbs. Gibbs formulated the law of the degradation of energy, or the second law of thermodynamics. It states that thermodynamic degradation is irrevocable over time: e.g., a burned log cannot be unburned. This law states that “even though there is an equivalence between a certain amount of work and a certain amount of heat, yet in any cyclic process, where a system is restored to its original state, there can never be a net conversion of heat into work, but the reverse is always possible.” That is, one cannot convert an amount of heat into its equivalent amount of work, without other changes taking place in the system. These changes, expressed statistically, constitute a passing of the system from ordered arrangement into more chaotic or random distribution. The disorder, disorganization, lack of patterning, or randomness of organization of a system is known as its entropy (S). It is the amount of progress of a system from improbable to probable states. The unit in which it is measured empirically is ergs or joules per degree absolute.
It was noted by Wiener [Cybernetics] and by Shannon that the statistical measure for the negative of entropy is the same as that for information, which Schrodinger [What Is Life?] has called “negentropy.” Discussing this relationship Rapoport says:
In classical thermodynamics, entropy was expressed in terms of the heat and the temperature of the system. With the advent of the kinetic theory of matter, an entirely new approach to thermodynamics was developed. Temperature and heat are now pictured in terms of the kinetic energy of the molecules comprising the system, and entropy becomes a measure of the probability that the velocities of the molecules and other variables of a system are distributed in a certain way. The reason the entropy of a system is greatest when its temperature is constant throughout is because this distribution of temperatures is the most probable. Increase of entropy was thus interpreted as the passage of a system from less probable to more probable states.
A similar process occurs when we shuffle a deck of cards. If we start with an orderly arrangement, say the cards of all the suits following each other according to their value, the shuffling will tend to make the arrangement disorderly. But if we start with a disorderly arrangement, it is very unlikely that through shuffling the cards will come into an orderly one. [What Is Information?]
One evening in Puerto Rico I observed a concrete illustration of how information decreases as entropy progresses. Epiphany was being celebrated according to Spanish custom. On the buffet table of a large hotel stood a marvelous carving of the three kings with their camels, all done in clear ice. As the warm evening went on, they gradually melted, losing their precise patterning or information as entropy increased. By the end of the evening the camels’ humps were nearly gone and the wise men were almost beardless.
Since, according to the second law, a system tends to increase in entropy over time, it must tend to decrease in negentropy or information. There is therefore no principle of the conservation of information as there are principles of the conservation of matter and energy. The total information can be decreased in any system without increasing it elsewhere, but it cannot be increased without decreasing it elsewhere. Making one or more copies of a given informational pattern does not increase information overall, though it may increase the information in the system which receives the copied information. Writing an original poem or painting a new picture or composing a new concerto does not create information overall, but simply selects one of many possible patterns available to the medium. Creating or transmitting such patterns can have great influence on the processes in any receiver of the pattern, but this is an impact of the meaning in the pattern not the information itself. Of course the information must be transmitted for the meaning to be transmitted.
3.1 Information and entropy.
At least three sorts of evidence suggest that the relationship between information and entropy is more than a formal identity based simply on similar statistical characteristics. First, Szilard wrote a paper about Maxwell’s sorting demon, which constituted a paradox for physicists since 1871. This is a mythical being
. . . whose faculties are so sharpened that he can follow every molecule in its course, such a being whose attributes are still as essentially finite as our own, would be able to do what is at present impossible to us. . . . Now let us suppose that. . . a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower ones to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.
Szilard made important progress in resolving Maxwell’s paradox by demonstrating that the demon transforms information into negative entropy. Using thermodynamics and quantum mechanics he calculated the minimum amount of energy required to transmit one bit of information, i.e., the minimum marker. Comparable calculations of the smallest possible amount of energy used in observing one bit of information were carried out by Brillouin. His work was based on the assertion that unless there is light the demon cannot “see” the molecules, and if that light is introduced into the system the entropy in it increases. This supports the second law. Like Szilard, Brillouin employed the statistics of thermodynamics and quantum mechanics. It is clear that he believed his work to apply both to microsystems and to macrosystems.
Calculations of the amount of information in various inorganic and organic chemical compounds have been made by Valentinuzzi and Valentinuzzi. They calculated that in order to organize one bit of information in a compound approximately 10-12 erg per bit is required. They suggested that such methods could be applied to calculations of the amount of information accumulated by living systems throughout growth.
Other relevant material can be found in a discussion by Foster, Rapoport, and Trucco, of work by Prigogine, De Groot, and others on an unresolved problem in thermodynamics of open systems. They turn their attention to the concept of Prigogine that in an open system (that is one in which both matter and energy can be exchanged with the environment) the rate of entropy production within the system, which is always positive, is minimized when the system is in a steady state. This appears to be a straightforward generalization of the second law, but after studying certain electrical circuits they conclude that this theorem does not have complete generality, and that in systems with internal feedbacks, internal entropy production is not always minimized when the system is in a stationary state. In other words, feedback couplings between the system parameters may cause marked changes in the rate of development of entropy. Thus it may be concluded that the “information flow” which is essential for this feedback markedly alters energy utilization and the rate of development of entropy, at least in some such special cases which involve feedback control. While the explanation of this is not clear, it suggests an important relationship between information and entropy.
The other evidence is the work of Pierce and Cutler, who calculated the minimum amount of energy used in transmitting one bit of information, the minimum marker, in macrosystems. They arrived at the same value that Szilard and Brillouin independently derived for microsystems. In a communication channel with thermal noise the minimum value was calculated by Pierce and Cutler as 9.56 x 10-24 J per bit per K. At the body temperature of a human being (37.0°C), for example, this would be 2.96 x 10-21 J per bit. Their approach to this question was to determine how much energy is required to overcome the thermal noise in a channel, which is the unpatterned, random motion of the particles in it. Thermal noise is referred to as “white” noise, that is all frequencies are equally represented in it up to the frequency of W cycles per second, W being its bandwidth. Also it is referred to as Gaussian, which means that if a large number of samples of it are taken, each of the 2W samples per second from it is uncorrelated and independent. Knowing N, the average energy of certain samples, does not help in predicting the energy of others. If 2WT (where T is a duration in time) is a large number of samples, however, the total energy of 2WT samples will be very close to 2WTN. Noise has the statistical character of entropy. In auditory transmission this random motion of particles in channels is heard as noise, and in visual transmission, as in television, it is seen as “snow” on the screen.
The amount of this noise times the length of the channel determines the amount of energy required to increase the signal above the noise and transmit the information. Several factors must be taken into consideration:
Take, for example, a satellite which is sending information. First of all, there is the “housekeeping” energy required to hold the molecules of the system together and keep it operating, maintaining the transmissions along the channel. In a satellite this involves the energy in the atoms and that holding together the molecules, as well as the energy stored in the batteries which operate the transmitter, and so forth. Then the level of thermal noise in the channel must be considered. At lower temperatures this is less, so that less energy is required to transmit information over the noise. The energy expended around absolute zero is very much less. Therefore we must calculate the temperature of any channel above absolute zero and compute from this a factor by which to multiply the minimal amount of energy required to transmit information at absolute zero. Furthermore, another factor must be allowed for the lack of efficiency in whatever coding is used, the degree to which the code is less than optimal. By calculations of this sort, Shannon figured the upper and lower bounds of the error probability in decoding optimal codes for a continuous channel with an additive Gaussian noise and subject to an average power limitation at the transmitter. Also transmitting systems ordinarily are not optimally efficient, achieving only a certain percentage of the highest possible efficiency. This means that they will need proportionately more energy to accomplish the transmission.
Of course the amount of energy actually required to transmit the information in the channel is a minute part of the total energy in the system, the “housekeeping energy” being by far the largest part of it. For this reason it seems almost irrelevant to compare the efficiency of various information processing systems by comparing the energies they require to transmit similar amounts of information. This can be done only in situations in which other factors accounting for more of the energy use can be held constant, or in which the parts of the system directly involved with the transmission are considered while all other parts are neglected. That is, such calculations may be important to one studying a single neuron, but when the whole brain or the entire body is considered, so many other “housekeeping” uses of energy appear that the slight changes in energy arising from information transmission may be unrecognizably small.
For such reasons information theorists tend to neglect the calculation of energy costs, so missing an important aspect of systems theory. In recent years systems theorists have been fascinated by the new ways to study and measure information flows, but matter-energy flows are equally important. Systems theory is more than information theory, since it must also deal with energetics – such matters as the muscular movements of people, the flow of raw materials through societies, or the utilization of energy by brain cells.
Only a minute fraction of the energy used by most living systems is employed for information processing. Nevertheless it may well be possible in specific experimental situations to determine rigorously the minimal amount of energy required to transmit one bit of information, and so to determine for such systems a constant relationship among measures of energy, entropy, and information.
I have noted above that the movement of matter-energy over space, action, is one form of process. Another form of process is information processing or communication, which is the change of information from one state to another or its movement from one point to another over space.
Communications, while being processed, are often shifted from one matter-energy state to another, from one sort of marker to another. If the form or pattern of the signal remains relatively constant during these changes, the information is not lost. For instance, it is now possible to take a chest x-ray, storing the information on photographic film; then a photoscanner can pass over the film line by line, from top to bottom, converting the signals to pulses in an electrical current which represent bits; then those bits can be stored in the core memory of a computer; then those bits can be processed by the computer so that contrasts in the picture pattern can be systematically increased; then the resultant altered patterns can be displayed on a cathode-ray tube and photographed. The pattern of the chest structures, the information, modified for easier interpretation, has remained largely invariant throughout all this processing from one sort of marker to another. Similar transformations go on in living systems.
One basic reason why communication is of fundamental importance is that informational patterns can be processed over space and the local matter-energy at the receiving point can be organized to conform to, or comply with, this information. As I have already said, if the information is conveyed on a relatively small, light, and compact marker, little energy is required for this process. Thus it is a much more efficient way to accomplish the result than to move the entire amount of matter-energy, organized as desired, from the location of the transmitter to that of the receiver. This is the secret of success of the delivery of “flowers by telegraph.” It takes much less time and human effort to send a telegram from London to Paris requesting a florist in the latter place to deliver flowers locally, than it would to drive or fly with the flowers from London to Paris.
Shannon was concerned with mathematical statements describing the transmission of information in the form of signals or messages from a sender to a receiver over a channel such as a telephone wire or a radio band. These channels always contain a certain amount of noise. In order to convey a message, signals in channels must be patterned and must stand out recognizably above the background noise.
Matter-energy and information always flow together. Information is always borne on a marker. Conversely there is no regular movement in a system unless there is a difference in potential between two points, which is negative entropy or information. Which aspect of the transmission is most important depends upon how it is handled by the receiver. If the receiver responds primarily to the material or energic aspect, I shall call it, for brevity, a matter-energy transmission; if the response is primarily to the information, I shall call it an information transmission. For example, the banana eaten by a monkey is a nonrandom arrangement of specific molecules, and thus has its informational aspect, but its use to the monkey is chiefly to increase the energy available to him. So it is an energy transmission. The energic character of the signal light that tells him to depress the lever which will give him a banana is less important than the fact that the light is part of a nonrandom, patterned organization which conveys information to him. So it is an information transmission. Moreover, just as living systems must have specific forms of matter-energy, so they must have specific patterns of information. For example, some species of animals do not develop normally unless they have appropriate information inputs in infancy. Monkeys cannot make proper social adjustment unless they interact with other monkeys during a period between the third and sixth months of their lives as Harlow showed. This treatment of the relationships of information and entropy can be epitomized by the Table: Information versus Entropy
Information versus Entropy
| H | = | – S |
|---|---|---|
| Information | Uncertainty | |
| Negentropy | Entropy | |
| Signal | Noise | |
| Accuracy | Error | |
| Form | Chaos | |
| Regularity | Randomness | |
| Pattern of form | Lack of pattern or formlessness | |
| Order | Disorder | |
| Organization | Disorganization | |
| Regular complexity | Irregular simplicity | |
| Heterogeneity | Homogeneity | |
| Improbability (only one alternative correctly describes the form) | Probability (More than one one alternative correctly describes the form) | |
| Predictability (only one alternative correctly describes the form) | Unpredictability (More than one alternative correctly describes the form) |
It indicates that there are several pairs of antonyms used in this section, one member of which is associated with the concept of information (H) and the other member of which is associated with its negative, entropy (S). Some of these are precise, technical terms. Others are commonsense words which may be more vague. Noting that such terms as regularity, pattern, and order are listed in the column under information, one might ask if there is not less rather than more information in a system with highly redundant pattern, order, or regularity. The answer is that information about a small portion of such an arrangement provides much understanding of the total system, which is not true of an arrangement characterized by randomness, lack of pattern, or disorder.
4. System
The term system has a number of meanings. There are systems of numbers and of equations, systems of value and of thought, systems of law, solar systems, organic systems, management systems, command and control systems, electronic systems, even the Union Pacific Railroad system. The meanings of “system” are often confused. The most general, however, is: A system is a set of interacting units with relationships among them [Ludwig von Bertalanffy] .The word “set” implies that the units have some common properties. These common properties are essential if the units are to interact or have relationships. The state of each unit is constrained by, conditioned by, or dependent on the state of other units. The units are coupled. Moreover, there is at least one measure of the sum of its units which is larger than the sum of that measure of its units.
4.1 Conceptual system
4.1.1 Units.
Units of a conceptual system are terms, such as words (commonly nouns, pronouns, and their modifiers), numbers, or other symbols, including those in computer simulations and programs.
4.1.2 Relationships. A relationship of a conceptual system is a set of pairs of units, each pair being ordered in a similar way. For example, the set of all pairs consisting of a number and its cube is the cubing relationship. Relationships are expressed by words (commonly verbs and their modifiers), or by logical or mathematical symbols, including those in computer simulations and programs, which represent operations, e.g., inclusion, exclusion, identity, implication, equivalence, addition, subtraction, multiplication, or division. The language, symbols, or computer programs are all concepts and always exist in one or more concrete systems, living or nonliving. The conceptual systems of science exist in one or more scientific observers, theorists, experimenters, books, articles, and/or computers.
4.1.3 The observer. The observer, for his own purposes and on the basis of his own characteristics, selects, from an infinite number of units and relationships, particular sets to study.
4.1.4 Variable. Each member of such a set becomes a variable of the observer’s conceptual system. He may select variables from the infinite number of units and relationships which exist in any concrete system or set of concrete systems, or on the other hand he may select variables which have no connection with any concrete system. His conceptual system may be loose or precise, simple or elaborate.
4.1.5 Indicator. An indicator is an instrument or technique used to measure fluctuations of variables in concrete systems.
4.1.6 Function. A function is a correspondence between two variables, x and y, such that for each value of x there is a definite value of y, and no two y’s have the same x, and this correspondence is: determined by some rule (e.g., x2 = y, xn = y, x + 3 = y). Any function is a simple conceptual system. Conceptual systems also may be very complex, involving many interrelated functions. This sense of “function” is the usual mathematical usage. In a concrete system this word has a different meaning.
4.1.7 Parameter. An independent variable through functions of which other functions may be expressed.
4.1.8 The state of a conceptual system. This state is the set of values on some scale, numerical or otherwise, which its variables have at a given instant. This state may or may not change over time.
4.1.9 Formal identity. One system may have one or more variables, each of which varies comparably to a variable in another system. If these comparable variations are so similar that they can be expressed by the same function, a formal identity exists between the two systems. H different functions are required to express the variations, there is a formal disidentity.
4.1.10 Relationships between conceptual and other sorts of systems. A conceptual system may be purely logical or mathematical, or its terms and relationships may be intended to have some sort of formal identity or isomorphism with units and relationships empirically determinable by some operation carried out by an observer, which are selected observable variables in a concrete system or an abstracted system. The observer selects the variables of his conceptual system. As to the many other variables in the concrete or abstracted system that are not isomorphic with the selected variables in his conceptual system, the observer may either (a) observe that they remain constant, or (b) operate on the concrete or abstracted system in order to ensure that they remain constant, or (c) “randomize them” i.e., assume without proof that they remain constant, or (d) simply neglect them.
Science advances as the formal identity or isomorphism increases between a theoretical conceptual system and objective findings about concrete or abstracted systems.
The chief purpose of this book is to state in prose a conceptual system concerning variables – units and relationships – which have important formal identities or isomorphisms to concrete, living systems.
4.2 Concrete system.
A concrete, real, or veridical system is a nonrandom accumulation of matter-energy, in a region in physical space-time, which is organized into interacting interrelated subsystems or components.
4.2.1 Units. The units (subsystems, components, parts, or members) of these systems are also concrete systems.
4.2.2 Relationships. Relationships in concrete systems are of various sorts, including spatial, temporal, spatiotemporal, and causal.
Both units and relationships in concrete systems are empirically determinable by some operation carried out by an observer. In theoretical verbal statements about concrete systems, nouns, pronouns, and their modifiers typically refer to concrete systems, subsystems, or components; verbs and their modifiers usually refer to the relationships among them. There are numerous examples, however, in which this usage is reversed and nouns refer to patterns of relationships or processes, such as “nerve impulse,” “reflex,” “action,” “vote,” or “annexation.”
4.2.3 The observer of a concrete system. The observer, according to Campbell, distinguishes a concrete system from unorganized entities in its environment by the following criteria: (a) physical proximity of its units; (b) similarity of its units; (c) common fate of its units; and (d) distinct or recognizable patterning of its units.
He maintains that evolution has provided human observers with remarkable skill in using such criteria for rapidly distinguishing concrete systems. Their boundaries are discovered by empirical operations available to the general scientific community rather than set conceptually by a single observer.
4.2.4 Variable of a concrete system. Any property of a unit or relationship within a system which can be recognized by an observer who chooses to attend to it, which can potentially change over time, and whose change can potentially be measured by specific operations, is a variable of a concrete system. Examples are the number of its subsystems or components, its size, its rate of movement in space, its rate of growth, the number of bits of information it can process per second, or the intensity of a sound to which it responds. A variable is intrasystemic, and is not to be confused with intersystemic variations which may be observed among individual systems, types, or levels.
4.2.6 Open system. Most concrete systems have boundaries which are at least partially permeable, permitting sizable magnitudes of at least certain sorts of matter-energy or information transmissions to pass them. Such a system is an open system. In open systems entropy may increase, remain in steady state, or decrease.
4.2.7 Closed system. A concrete system with impermeable boundaries through which no matter-energy or information transmissions of any sort can occur is a closed system. This is a special case, in which inputs and outputs are zero, of the general case of open systems. No actual concrete system is completely closed, so concrete systems are either relatively open or relatively closed. In closed systems, entropy generally increases, exceptions being when certain reversible processes are carried on which do not increase it. It can never decrease. Whatever matter-energy happens to be within the system is all there is going to be, and it gradually becomes disordered. A body in a hermetically sealed casket, for instance, slowly crumbles and its component molecules become intermingled. Separate layers of liquid or gas in a container move toward random distribution. Gravity may prevent entirely random arrangement.
4.2.8 Nonliving system. Every concrete system which does not have the characteristics of a living system is a nonliving system. Nonliving systems constitute the general case of concrete systems, of which living systems are a very special case. Nonliving systems need not have the same critical subsystems as living systems, though they often have some of them.
4.2.9 Living system. The living systems are a special subset of the set of all possible concrete systems. They are composed of the monerans, protistans, fungi, plants, animals, groups, organizations, societies, and supranational systems. They all have the following characteristics:
(a) They are open systems, with significant inputs, throughputs, and outputs of various sorts of matter-energy and information.
(b) They maintain a steady state of negentropy even though entropic changes occur in them as they do everywhere else. This they do by taking in inputs of foods or fuels, matter-energy higher in complexity or organization or negentropy, i.e., lower in entropy, than their outputs. The difference permits them to restore their own energy and repair breakdowns in their own organized structure. Schrodinger said that “What an organism feeds upon is negative entropy. ” [What Is Life?] In living systems many substances are produced as well as broken down; gradients are set up as well as destroyed; learning as well as forgetting occurs. To do this such systems must be open and have continual inputs of matter-energy and information. Walling off living systems to prevent exchanges across their boundaries results in what Brillouin calls” death by confinement.” Since the second law of thermodynamics is an arrow pointing along the one-way road of the inevitable forward movement which we call time, entropy will always increase in walled-off living systems. The consequent disorganization will ultimately result in the termination of the system but the second law does not state the rate at which dissolution approaches. The rate might even be zero for a time; the second law has no time limit.
(c) They have more than a certain minimum degree of complexity.
(d) They either contain genetic material composed of deoxyribonucleic acid (DNA), presumably descended from some primordial DNA common to all life, or have a charter. One of these is the template – the original “blueprint” or “program” – of their structure and process from the moment of their origin.
(e) They are largely composed of an aqueous suspension of macromolecules, proteins constructed from about 20 amino acids and other characteristic organic compounds, and may also include nonliving components.
(f) They have a decider, the essential critical sub-system which controls the entire system, causing its subsystems and components to interact. Without such interaction under decider control there is no system.
(g) They also have certain other specific critical sub-systems or they have symbiotic or parasitic relationships with other living or nonliving systems which carry out the processes of any such subsystem they lack.
(h) Their subsystems are integrated together to form actively self-regulating, developing, unitary systems with purposes and goals.
(i) They can exist only in a certain environment. Any change in their environment of such variables as temperature, air pressure, hydration, oxygen content of the atmosphere, or intensity of radiation, outside a relatively narrow range which occurs on the surface of the earth, produces stresses to which they cannot adjust. Under such stresses they cannot survive.
4.2.10 Totipotential system. A living system which is capable of carrying out all critical subsystem processes necessary for life is totipotential. Some systems are totipotential only during certain periods their existence. For instance, a chick at hatching cannot lay an egg, even though chickens are a precocious species that can take care of themselves as soon as they hatch. The chick, therefore, should not be called totipotential until it has matured to henhood and its reproducer subsystem is functional.
4.2.11 Partipotential system. A living system which does not itself carry out all critical subsystem processes is partipotential. It is a special case of which the totipotential system is the general case. A partipotential system must interact with other systems that can carry out the processes which it does not, or it will not survive. To supply the missing processes, partipotential systems must be parasitic on or symbiotic with other living or nonliving systems.
4.2.12 Fully functioning system. A system is fully functioning when it is carrying out all the processes of which it is capable.
4.2.13 Partially functioning system. A system is partially functioning when it is carrying out only some of the processes of which it is capable. If it is not carrying out all the critical subsystem processes, it cannot survive, unless it is parasitic on or symbiotic with some other system which supplies the other processes. Furthermore it must do its own deciding, or it is not a system.
4.3 Abstracted system
4.3.1 Units. The units of abstracted systems are relationships abstracted or selected by an observer in the light of his interests, theoretical viewpoint, or philosophical bias. Some relationships may be empirically determinable by some operation carried out by the observer, but others are not, being only his concepts.
4.3.2 Relationships. The relationships mentioned above are observed to inhere and interact in concrete, usually living, systems. In a sense, then, these concrete systems are the relationships of abstracted systems. The verbal usages of theoretical statements concerning abstracted systems are often the reverse of those concerning concrete systems: the nouns and their modifiers typically refer to relationships and the verbs and their modifiers (including predicates) to the concrete systems in which these relationships inhere and interact. These concrete systems are empirically determinable by some operation carried out by the observer. A theoretical statement oriented to concrete systems typically would say, “Lincoln was President,” but one oriented to abstracted systems, concentrating on relationships or roles, would very likely be phrased, “The Presidency was occupied by Lincoln.”
An abstracted system differs from an abstraction, which is a concept (like those that make up conceptual systems) representing a class of phenomena all of which are considered to have some similar “class characteristic.” The members of such a class are not thought to interact or be interrelated, as are the relationships in an abstracted system.
Abstracted systems are much more common in social science theory than in natural science. Since abstracted systems usually are oriented toward relationships rather than toward the concrete systems which have those relationships, spatial arrangements are not usually emphasized. Consequently their physical limits often do not coincide spatially with the boundaries of any concrete system, although they may. Speaking of system hierarchies, Simon says:
There is one important difference between the physical and biological hierarchies, on the one hand, and social hierarchies, on the other. Most physical and biological hierarchies are described in spatial terms. We detect the organelles in a cell in the way we detect the raisins in the cake – they are ‘visibly’ differentiated substructures localized spatially in the larger structure. On the other hand, we propose to identify social hierarchies not by observing who lives close to whom but by observing who interacts with whom. These two points of view can be reconciled by defining hierarchy in terms of intensity of interaction, but observing that in most biological and physical systems relatively intense interaction implies relative spatial propinquity. One of the interesting characteristics of nerve cells and telephone wires is that they permit very specific strong interactions at great distances. To the extent that interactions are channeled through specialized communications and transportation systems, spatial propinquity becomes less determinative of structure. [The Architecture of Complexity, 1962]
There are other reasons why abstracted systems are sometimes preferred to concrete. Functionalists may resist the use of space-time coordinates because they seem static. But one must have such coordinates in order to observe and measure process. Subjectivists may resist such coordinates because their private experience does not seem to be presented to them in external space-time. But where else do their inputs arise from?
Parsons has attempted to develop general behavior theory using abstracted systems. An interesting colloquy at a conference on unified theory conducted by Grinker spells out ways in which a theory developed around abstracted systems differs from one using concrete systems. Ruesch, Parsons, and Rapoport are speaking:
RUESCH: Previously I defined culture as the cumulative body of knowledge of the past, contained in memories and assumptions of people who express this knowledge in definite ways. The social system is the actual habitual network of communication between people. If you use the analogy of the telephone line, it corresponds to actual calls made. The society is the network – the whole telephone network. Do you agree with these definitions?
PARSONS: No, not quite. In the limiting conception a society is composed of human individuals, organisms; but a social system is not, and for a very important reason, namely, that the unit of a partial social system is a role and not the individual.
RAPOPORT: The monarch is not an individual, but is a site into which different individuals step. Is that your unit of the social system?
PARSONS: Yes. A social system is a behavioral system. It is an organized set of behaviors of persons interacting with each other: a pattern of roles. The roles are the units of a social system. We say, ‘John Jones is Mary Jones’ husband’ He is the same person who is the mail carrier, but when we are talking about the mail carrier we are abstracting from his marriage relationship. So the mail carrier is not a person, just a role. On the other hand, the society is an aggregate of social subsystems, and as a limiting case it is that social system which comprises all the roles of all the individuals who participate.
What Ruesch calls the social system is something concrete in space-time, observable and presumably measurable by techniques like those of natural science. To Parsons the system is abstracted from this, being the set of relationships which are the form of organization. To him the important units are classes of input-output relationships of subsystems rather than the subsystems themselves.
Grinker accurately described this fundamental, but not irresolvable, divergence when he made the following comment:
Parsons stated that. . . [action] is not concerned with the internal structure of processes of the organism, but is concerned with the organism as a unit in a set of relationships and the other terms of that relationship, which he calls situation. From this point of view the system is a system of relationship in action, it is neither a physical organism nor an object of physical perception. On the other hand, some of us consider that the foci or systems which are identified in a living field must be considered as being derived through evolution, differentiation and growth from earlier and simpler forms and functions and that within these systems there are capacities for specializations and gradients. Sets of relationships among dimensions constitute a high level of generalization that can be more easily understood if the physical properties of its component parts and their origins and ontogenetic properties are known.
4.4 Abstracted versus concrete systems.
One fundamental distinction between abstracted and concrete systems is that the boundaries of abstracted systems may at times be conceptually established at regions which cut through the units and relationships in the physical space occupied by concrete systems, but the boundaries of these latter systems are always set at regions which include within them all the units and internal relationships of each system. To some it may appear that another distinction between concrete and abstracted systems is something like the difference between saying “A has the property r” and saying “r is a property of A.” This translation is logically trivial. In empirical science, however, there can be an important difference between discovering that A has the property r and finding an A which has the property r.
It is possible to assert connections in abstracted systems among all sorts of entities, like or unlike, near together or far apart, with or without access to each other in space – even Grandpa’s moustache, Japanese haiku poetry, and the Brooklyn Bridge – depending upon the particular needs of a given project. How and why this is done will determine whether the rest are trivial, like a sort of intellectual “Rube Goldberg apparatus,” or whether they are functional.
A science of abstracted systems certainly is possible and under some conditions may be useful. When Euclid was developing geometry, with its practical applications to the arrangement of Egyptian real estate, it is probable that the solid lines in his figures were originally conceived to represent the borders of land areas or objects.
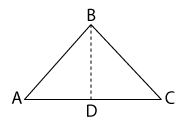
Sometimes, he would use dotted “construction lines” to help conceptualize a geometric proof. The dotted line did not correspond to any actual border in space. Triangle ABD could be shown to be congruent to triangle CBD and therefore the angle BAD could be proved to equal the angle BCD. After the proof was completed, the dotted line might well be erased, since it did not correspond to anything real and was useful only for the proof. Such construction lines, representing relationships among real lines, were used in the creation of early forms of abstracted systems.
If the diverse fields of science are to be unified, it would be helpful if all disciplines were oriented either to concrete or to abstracted systems. It is of paramount importance for scientists to distinguish clearly between them. To use both kinds of systems in theory, leads to unnecessary problems. It would be best if one type of system or the other were generally used in all disciplines. Past tradition is not enough excuse for continuing to use both. Since one can conceive of relationships between any concrete system and any other, one can conceive of many abstracted systems which do not correspond to any reality. The existence of such systems is often asserted in science, and empirical studies frequently show there really are no such systems.
Confusion of abstracted and concrete systems has resulted in the contention that the concept of system is logically empty because one cannot think of anything or any collection of things which could not be regarded as a system. What is not a concrete system? Any set of subsystems or components in space-time which do not interact, which do not have relationships in terms of the variables under consideration, is not a concrete system. Physicists call it a heap. My heart and your stomach, together, are not a concrete system; the arrangements of cells in your fingernails and in your brown felt hat are not a concrete system; the light streaming through my study window and the music floating out from my stereo are not a concrete system. All the coal miners in Wales were not a concrete system until they were organized into an intercommunicating, interacting trade union. Sherlock Holmes did not assume that red-haired men in general were a concrete system, but when he got evidence that some of them were interacting, he deduced the existence of an organized Red-Headed League.
When abstracted systems are used it is essential that they be distinguished from abstractions. Is “culture” an abstraction, the class of all stored and current items of information which are shared in common by certain individuals who are members of a group, organization, society, or supranational system, as revealed by similarities of those persons’ customary behavior or of their artifacts – art objects, language, or writings? Or does the term culture imply interactions among those items of information, so representing an abstracted system? Or, to take another example, is an individual’s “personality” merely a class of traits as represented by repeated similar acts, gestures, and language of a person, or does it imply interactions among these traits, which would be an abstracted system? Terms like culture or personality can be useful in behavioral science to refer to commonalities among people or among characteristics of a single person, but they must be used unambiguously as either an abstraction or an abstracted system.
No scientist, in social science or any field, will change his traditional procedures without reason. There are, however, a number of simple, down-to-earth practical reasons why theorists should focus upon concrete systems rather than abstracted systems, as Etzioni has suggested. [The Active Society, 1968]
(a) In the first place concrete systems theory is easier to understand. Our sense organs reify, distinguishing objects from their environment. Since childhood concrete objects (“mamma,” “cup”) have been the nouns of most of our sentences, and words representing relationships or changes in relations (“loves,” “runs”) have been the verbs. We are used to seeing the world as a collection of concrete objects in space-time, and these objects naturally draw our attention. Relationships are less obvious. Abstracted systems oriented toward relationships are unnecessarily complicated for our ordinary thinking processes. We are used to putting things into the framework of space and time. It helps us orient them accurately to other things. Movies which jump around in time puzzle us. We are confused when the action of a novel or play skips about in space from one place to another. For general theory embracing biological and social aspects of life and behavior, conceptualizations referring to concrete systems in space-time enable us to profit from a lifetime of experience in thinking that way. Abstracted systems are usually at best inconvenient and clumsy conceptual tools. Spatial propinquity or accessibility to information transmitted over physical channels is essential for all social interactions, except those based on mutual agreements remembered from past interactions. Even then, spatial contact in the past is essential. Spatial orientation, therefore, is important, for both biological and social science: (1) It is a significant fact about cellular function that deoxyribonucleic acid (DNA) is found only in a cell’s nucleus and some other organelles. (2) The location of pain sensory tracts near the central canal of the human spinal cord explains why pain sensation is halted, in the bodily regions to which those tracts lead, when the disease process of syringomyelia widens the central canal until it transects the tracts. (3) The wings of the ostrich are of inadequate size to carry its large weight, so it must run rather than fly. (4) That the spatial positions of jury members around the table significantly affected their behaviors was shown by Stodtbeck and Hook. (5) The groups which make up organizations interact most frequently and most effectively when they are close together in space. Differences in proximity of houses in two Costa Rican villages were found by Powell to be associated with differences between the two villages in the frequency of visiting among families. In the village in which the houses were close to each other, 53 percent of the visiting occurred daily; in the more open village only 34 percent was daily. (6) It is well recognized by sociologists, economists, and political scientists that many sorts of behaviors differ in rural regions and in urban areas. (7) International relations are often affected by the spatial locations and geographical characteristics of nations and the relationships of their land masses, their bodies of water, and the seas around them. The histories of the Panama Canal or the Suez Canal, of Switzerland or Cyprus attest to such geopolitical factors.
(b) Variations in the units of systems appear to contribute as much more to the total variance in the systems than variations in their relationships, although of course the total system variance arises from both, plus interactions between the two. Any cell in a given location at a given time, any ruler of a given nation in a given period, receives comparable matter-energy and information inputs. But they may act quite differently. If their inputs or relationships vary, of course their actions vary. Process of systems is explained only when we take account of both units and relationships of cells and the internal environment around them, of the leader and the Zeitgeist.
(c) Theory which deals with concrete systems avoids two common sorts of confusion. One is the confusion of conceptualizations which seem to assume that information can be transmitted from system to system without markers to bear it. The other is the confusion of some social science theories which appear to assume that actions, roles, or relationships carry on a life of their own, independent of other aspects of the people or other concrete systems whose processes they are. When the head of a brokerage firm, who is also a Sunday school teacher, in his role as chairman of the board connives with the bookkeeper in an embezzlement, the chairman takes the Sunday school teacher right along with him into jail. They are aspects of the process of a concrete system in a suprasystem.
(d) If a surgeon does not cut along planes of cleavage, he may become confused about spatial relations as he gets farther and farther into a region like, for instance, the pelvis. Not only is it harder for him to reconstruct firm muscles when he sews up again, but it is more difficult for him to conceptualize the relationship between different structures. Behavioral scientists, if they deal with abstracted systems and establish their own conceptual boundaries which cut across concrete systems, easily forget the intrasystem relationships in concrete systems which influence processes within and among those systems. Consequently their understanding of the phenomena they study is often incomplete and inaccurate.
(e) If the social sciences were to formulate their problems, whenever possible, in the way which has proved most convenient for the natural sciences over centuries, unification of all the sciences would be accelerated.
4.5 Abstracted versus conceptual systems.
Because some of the relationships in abstracted systems are selected by scientific observers, theorists, and/or experimentalists, it is possible that they might be confused with conceptual systems, since both units and relationships of conceptual systems are so selected. The two kinds of systems differ in that some units and/or relationships of every abstracted system are empirically determined and this is not true of any conceptual system.
All three meanings of “system” are useful in science, but confusion results when they are not differentiated. A scientific endeavor may appropriately begin with a conceptual system and evaluate it by collecting data on a concrete or on an abstracted system, or it may equally well first collect the data and then determine what conceptual system they fit. Throughout this book the single word system, for brevity, will always mean “concrete system.” The other sorts of systems will always be explicitly distinguished as either “conceptual system” or “abstracted system.”
5. Structure
The structure of a system is the arrangement of its subsystems and components in three-dimensional space at a given moment of time. This always changes over time. It may remain relatively fixed for a long period or it may change from moment to moment, depending upon the characteristics of the process in the system. This process halted at any given moment, as when motion is frozen by a high-speed photograph, reveals the three-dimensional spatial arrangement of the system’s components as of that instant. For example, when anatomists investigate the configuration of the lobules of the liver, they study dead, often fixed, material in which no further activity can be expected to occur. Similarly geographers may study the locations of the populations in the cities of China and its interconnecting routes of travel in the year 1850. These are studies of structure. Time slices at a given moment reveal spatial relations, but they do not indicate other aspects of the system. For instance they may show the positions of molecules but not their momenta, or the locations of members of a group but not their attractiveness to one another. Measures of these other aspects must be represented on the dimensions of other spaces, just as physicists may represent the locations of particles in three of the six dimensions of “phase space” and their forces or momenta in the other three.
When systems survive, maintaining steady states over prolonged periods, their structures are stable. Consequently the concept of stability is often confused with the concept of structure. Structure, of course, is easier to observe if it is stable, but the spatial organization of a system’s parts is its structure whether it changes slowly or rapidly. Anyone can define slowly changing process as “structure” and rapidly changing process as “function,” but when he does so he is using “structure” in a different sense than its most frequent usage in common speech or in natural science. These two quite separate meanings must not be confused. It is also vital to distinguish my use of the word structure from another scientific usage of the term to mean generalized patterning. This definition, which recognizes that information and structure are connected, states that the latter is an entire set of relations, as indicated by a form of nonmetric correlation, among any group of variables. This usage makes it possible to speak of the “structure of French,” the “structure of music” or the “structure of a nerve impulse” – conceptual patterns or patterns in time – as well as the “structure of a crystal” or the “structure of the pelvis” – patterns in space. It is a contribution to science to recognize that there is patterning among conceptual or temporal variables which is comparable to patterning among spatial variables. Indeed, spatial variables can be transformed to temporal, or vice versa, as when one plays a piano roll with a configuration of holes on a player piano, or when one records a dance in choreographic notation.
For empirical science, however, the distinctions between spatial and temporal dimensions, between physical space and conceptual spaces, must be maintained, and my definition of structure does so. The word is not used to mean stability, or to mean generalized patterning among any set of variables. It refers only to arrangements of components or subsystems in three-dimensional space.
6. Process
All change over time of matter-energy or information in a system is process. If the equation describing a process is the same no matter whether the temporal variable is positive or negative, it is a reversible process; otherwise it is irreversible, or better, less readily reversible. At least three sequential time slices of structure must be compared before reversible and irreversible or less readily reversible processes can be distinguished. Process includes the ongoing function of a system, reversible actions succeeding each other from moment to moment. This usage should not be confused with the mathematical usage of function defined earlier. Process also includes history, less readily reversed changes like mutations, birth, growth, development, aging, and death; changes which commonly follow trauma or disease; and changes resulting from learning which are not later forgotten. Historical processes alter both the structure and the function of the system. I have said “less readily reversed” instead of “irreversible” (although many such changes are in fact irreversible) because structural changes sometimes can be reversed: a component which has developed and functioned may atrophy and finally disappear with disuse; a functioning part may be chopped off a hydra and regrow. History, then, is more than the passage of time. It involves also accumulation in the system of residues or effects of past events (structural changes, memories, and learned habits). A living system carries its history with it in the form of altered structure, and consequently of altered function also. So there is a circular relation among the three primary aspects of systems – structure changes momentarily with functioning, but when such change is so great that it is essentially irreversible, a historical process has occurred, giving rise to a new structure.
I have differentiated carefully between structure and process, but often this is not done. Leighton has shown that the meanings of structure and function (or process) are not always clearly distinguished. He contends that what is meant by structure in the study of societies is what is ordinarily called function in the study of bodily organs. He lists components of a socio-cultural unit like a town as: “family, including extended families; neighborhoods; associations; friendship groups; occupational associations; institutions such as those concerned with industry, religion, government, recreation, and health; cultural systems; socioeconomic classes; and finally societal roles.” In my terminology not all of these are structural components. Some are abstractions about classes of processes, relationships, or abstracted systems.
Leighton says:
Components such as these and their arrangement in relation to each other are often called ‘structure’ by sociologists and anthropologists. This usage of the term parallels that of psychiatrists and psychologists when they speak of the ‘structure’ of personality in referring to the relationships of such components as the id, ego, and superego. In both instances the word means process. It stands for patterned events which tend to occur and recur with a certain amount of regularity. Hence, when one says that the structure of a community or a personality has such and such characteristics, he is, in effect, talking about an aspect of function.
It seems to me that’ structure’ as a term can be troublesome when one is trying to grasp and analyze the nature of sociocultural and psychological phenomena. This is probably not the case with those authors whose names are associated with the term, but in my experience it does confuse people new to the field, especially those from other disciplines trying to master the concepts and develop an understanding of both personality and sociocultural processes. Hence some impressions on the reasons for these difficulties may be worth recording.
The meaning attributed to ‘structure’ by sociologists, anthropologists, psychologists, and psychiatrists is one that is limited, denotative, and reasonably clear. Trouble arises from the fact that connotative meanings are carried over from other contexts in which the word has markedly different significance. For example, the usage with reference to personality and society is dynamic, while in anatomy, in architecture, and in many everyday contexts the word refers to the static aspect of things. A structure is not something which keeps coming back in a regular flow of movement like a figure in a dance; it is something which just sits there like a chair.
Another and more important connotation is that of substance. The overwhelming force of the word in everyday usage is of an entity which can be seen and felt. It is – relative to other experiences in living – something directly available to the senses. This common meaning is also found in many sciences, particularly biology. When one speaks of the structure of the heart he is talking about visible-palpable substance, not the rhythmical contractions. The latter are an aspect of its functioning. Yet it is precisely the analogue in behavior of these contractions, this regular functional process, that is meant when one speaks of ‘structure’ in a society. The brain offers another example. Its ‘structure’ consists in the arrangements that can be seen with and without the aid of instruments such as the microscope – cerebellum, medulla oblongata, layers of the cortex, and so on. The recurrent electrical events called brain waves are not considered structure, but rather a manifestation of functioning. Again, however, they are the kind of phenomena which in discussions of society are called ‘structure.’ The closest analogue in the community of the anatomical use of ‘structure’ is the arrangement of streets, houses, and other buildings.
A further point is this: in common terms, and also in biology, ‘structure’ is for the most part a description of observed nature, whereas in discussions of personality and society it is usually an inference from observed nature. No one, for instance, has ever seen a class system in the same sense in which the layers of the body can be seen – skin, fascia, muscles, etc. [A. H. Leighton, My name is legion: foundations for a theory of man in relation to culture, Basic Books, 1959]
The term structure appears so misleading to Leighton that he suggests it should perhaps not be used. He continues by saying that, in a personal communication, Hughes suggested to him that “’Structure’ refers to configurations which pre-exist other processes that are the focus of our attention – namely the ‘functions.'” Then he quotes Bertalanffy, who said:
The antithesis between structure and function, morphology and physiology is based upon a static conception of the organism. In a machine there is a fixed arrangement that can be set in motion but can also be at rest. In a similar way the pre-established structure of, say, the heart is distinguished from its function, namely rhythmical contraction. Actually this separation between a pre-established structure and processes occurring in the structure does not apply to the living organism. For the organism is the expression of an everlasting orderly process, though, on the other hand, this process is sustained by underlying structures and organized forms. What is described in morphology as organic forms and structures, is in reality a momentary cross-section through a spatio-temporal pattern.
What are called structures are slow processes of long duration, functions are quick processes of short duration. If we say that a function such as a contraction of a muscle is performed by a structure, it means that a quick and short process wave is superimposed on a long-lasting and slowly-running wave. [Ludwig von Bertalanffy, Problems of Life, 1952]
My terminology avoids this semantic morass. I agree with Leighton that the family, various groups, associations, and institutions are parts of the structure of a town or other such concrete system. The cultural systems, societal roles, and socioeconomic classes which Leighton refers to are, however, abstractions, relationships, or abstracted systems. Structure is the arrangement of a concrete system’s parts at a moment in three-dimensional space. Process is change in the matter-energy or information of that system over time. The two are entirely different and need not be confused.
7. Type
If a number of individual living systems are observed to have similar characteristics, they often are classed together as a type. Types are abstractions. Nature presents an apparently endless variety of living things which man, from his earliest days, has observed and classified – first, probably, on the basis of their threat to him, their susceptibility to capture, or their edibility, but eventually according to categories which are scientifically more useful. Classification by species is applied to free-living cells or organisms – monerans, protistans, fungi, plants, or animals – because of their obvious relationships by reproduction. These systems are classified together by taxonomists on the basis of likeness of structure and process, genetic similarity and ability to interbreed, and local interaction – often including, in animals, the ability to respond appropriately to each other’s signs. The individual members of a given species are commonly units of widely separated concrete systems. The reason the species is not a concrete system is that, though all its members can interbreed and interact, they do so only locally, and there is no overall species organization. Of course at some time in the past their ancestors did, but that may have been long ago. Complete isolation of one local set of members of a species from other local sets, after a time, may lead to the development of a new species because mutations occur in one local interbreeding set which are not spread to others of the species.
There are various types of systems at other levels of the hierarchy of living systems besides the cell and organism levels, each classed according to different structural and process taxonomic differentia which I discuss in later chapters. There are, for instance, primitive societies, agricultural societies, and industrial societies, just as there are epithelial cells, fibroblasts, red blood corpuscles, and white blood cells, as well as free-living cells. Biological interbreeding as a way of transmitting a new system’s template, which is a specialized form of information processing, does not occur at certain levels. At these levels – like the organization or society – it may well be, however, that the template, the “charter” information which originally “programmed” the structure and process of all individual cases of a particular type of system, had a common origin with all other templates of that type.
Types of systems often overlap one another along a given variable. Within one animal species, for instance, there may be individuals which are larger than many members of another species which on the average is much larger. Primitive societies in general have been less populous than agricultural societies, but there have been exceptions. Rank ordering of types is also different depending upon the variable. The rabbit, though larger, seems less intelligent than the rat. He has much larger ears – more like those of a horse in size – but a very much shorter and better upholstered tail.
8. Level
The universe contains a hierarchy of systems, each more advanced or “higher” level made of systems of lower levels. Atoms are composed of particles; molecules, of atoms; crystals and organelles, of molecules. About at the level of crystallizing viruses, like the tobacco mosaic virus, the subset of living systems begins. Viruses are necessarily parasitic on cells, so cells are the lowest level of living systems. Cells are composed of atoms, molecules, and multimolecular organelles; organs are composed of cells aggregated into tissues; organisms, or organs; groups (e.g., herds, flocks, families, teams, tribes), of organisms; organizations, of groups (and sometimes single individual organisms); societies, of organizations, groups, and individuals; and supranational systems, of societies and organizations. Higher levels of systems may be of mixed composition, living and nonliving. They include ecological systems, planets, solar systems, galaxies, and so forth. It is beyond my competence and the scope of this book to deal with the characteristics – whatever they may be – of systems below and above those levels which include the various forms of life, although others have done so. This book, in presenting general systems behavior theory, is limited to the subset of living systems – cells, organs, organisms, groups, organizations, societies, and supranational systems.
It would be convenient for theorists if the hierarchical levels of living systems fitted neatly into each other like Chinese boxes. The facts are more complicated, as my discussion of subsystems and components indicates. I have distinguished seven levels of living systems for analysis here, but I do not argue that there are exactly these seven, no more and no less. For example, one might conceivably separate tissue and organ into two separate levels. Or one might, as Anderson and Carter have suggested, separate the organization and the community into two separate levels – local communities, urban and rural, are composed of multiple organizations, just as societies are composed of multiple local communities, states, or provinces. Or one might maintain that the organ is not a level, since there are no totipotential organs.
What are the criteria for distinguishing any one level from the others? They are derived from a long scientific tradition of empirical observation of the entire gamut of living systems. This extensive experience of the community of scientific observers has led to a consensus that there are certain fundamental forms of organization of living matter-energy. Indeed the classical division of subject matter among the various disciplines of the life or behavior sciences is implicitly or explicitly based upon this consensus. Observers recognize that there are in the world many similar complexly organized accumulations of matter-energy, each identified by the characteristics I have already mentioned above: (a) Physical proximity of its units. (b) Similar size in physical space of its units, significantly different from the size of the units of the next lower or higher levels. (c) Similarity of its constituent units. Such organized accumulations of matter-energy have multiple constituent units, ordinarily a preponderance of their components, which are systems of the next lower level, i.e., just as molecules are made up of two or more atoms and atoms are composed of two or more particles, so groups are made up of two or more organisms, and organs are composed of two or more cells. This is the chief way to determine to what level any system belongs. Such nomenclature is comparable to standard procedure in physical science. For example, one does not call a system a crystal unless it is made of molecules composed of atoms. (d) Common fate of its units. And (e) distinctive structure and process of its units.
It is important to follow one procedural rule in systems theory, in order to avoid confusion. Every discussion should begin with an identification of the level of reference, and the discourse should not change to another level without a specific statement that this is occurring. Systems at the indicated level are called systems. Those at the level above are suprasystems, and those at the next higher level, suprasuprasystems. Below the level of reference are subsystems, and below them are subsubsystems. For example, if one is studying a cell, its organelles are the subsystems, and the tissue or organ is its suprasystem, unless it is a free-living cell whose suprasystem includes other living systems with which it interacts.
8. 1 Intersystem generalization.
A fundamental procedure in science is to make generalizations from one system to another on the basis of some similarity between the systems which the observer sees and which permits him to class them together. For example, since the nineteenth century, the field of “individual differences” has been expanded, following the tradition of scientists like Galton in anthropometry and Binet in psychometrics. In Fig. 2-2, states of separate
specific individual systems on a specific structural or process variable are represented by I1 to In. For differences among such individuals to be observed and measured, of course, a variable common to the type – along which there are individual variations – must be recognized (T1). Physiology depends heavily, for instance, upon the fact that individuals of the type (or species) of living organisms called cats are fundamentally alike, even though minor variations from one individual to the next are well recognized.
Scientists may also generalize from one type to another (T1 to Tn). An example is cross-species generalization, which has been commonly accepted only since Darwin. It is the justification for the patient labors of the white rat in the cause of man’s understanding of himself. Rats and cats, cats and chimpanzees, chimpanzees and human beings are similar in structure, as comparative anatomists know, and in function, as comparative physiologists and psychologists demonstrate.
The amount of variance among species is greater than among individuals within a species. If the learning behavior of cat Felix is compared with that of mouse Mickey, we would expect not only the sort of individual differences which are found between Mickey and Minnie Mouse, but also greater species differences. Cross-species generalizations are common, and many have good scientific acceptability, but in making them, interindividual and interspecies differences must be kept in mind. The learning rate of men is not identical to that of white rats, and no man learns at exactly the same rate as any other.
The third type of scientific generalization indicated in Fig. 2-2 is from one level to another. The basis for such generalization is the assumption that each of the levels of life, from cell to society, is composed of systems of the previous lower level. These cross-level generalizations will, ordinarily, have greater variance than the other sorts of generalizations since they include variance among types and among individuals. But they can be made, and they can have great conceptual significance.
That there are important uniformities, which can be generalized about, across all levels of living systems is not surprising. All are composed of comparable carbon-hydrogen-nitrogen constituents, most importantly a score of amino acids organized into similar proteins, which are produced in nature only in living systems. All are equipped to live in a water-oxygen world rather than, for example, on the methane and ammonia planets so dear to science fiction. Also they are all adapted only to environments in which the physical variables, like temperature, hydration, pressure, and radiation, remain within relatively narrow ranges. Moreover, they all presumably have arisen from the same primordial genes or template, diversified by evolutionary change. Perhaps the most convincing argument for the plausibility of cross-level generalization derives from analysis of this evolutionary development of living systems. Although increasingly complex types of living systems have evolved at a given level, followed by higher levels with even greater complexity, certain basic necessities did not change. All these systems, if they were to survive in their environment, had, by some means or other, to carry out the same vital subsystem processes. While free-living cells, like protozoans, carry these out with relative simplicity, the corresponding processes are more complex in multicellular organisms like mammals, and even more complex at higher levels. A directed graph (somewhat like an organization chart) was drawn by Rashevsky to indicate how these various processes are carried out by, or mapped on, particular structures in simple cells like protozoans. Then, the same processes are “shredded out” to multiple components in a more complex system at a higher level. This shredding-out is somewhat like the sort of division of labor which Parkinson made famous in his law (C. N. Parkinson, Parkinson’s Law, 1957). Each process is broken down into multiple subprocesses which are mapped upon multiple structures, each of which becomes specialized for carrying out a subprocess. If this allocation of processes is not to be chaotic in the more complex systems which have more components involved in each process, the rationale for their division of labor must be derived from that which prevailed in their simpler progenitor systems. This shred-out or mapping of comparable processes from simpler structures at lower levels to more complex structures at higher levels is a chief reason why I believe that cross-level generalizations will prove fruitful in the study of living systems. Cross-level comparisons among nonliving systems may not be so profitable, for they are not derived by any genetically determined evolutionary shred-out, and there is no clear evidence that to share a given environment, nonliving systems must have comparable structures and processes.
The shred-out principle has implications for scientific method. Every scientist’s academic freedom guarantees him the right to select his preferred procedures. We may, however, question the wisdom and responsibility of anyone who originates his own categorization or taxonomy of system processes without regard to the other such classifications developed by his colleagues working at his level. Yet this is often done. It is even commoner for a scientist to originate such a classification independent of those made at other levels of systems. This is more understandable, however, for unless one accepts the emphasis of general living systems theory on cross-level generalizations, recognizing that evolution requires that the processes of systems at higher levels have been shredded out by division of labor from those at lower levels, there is no reason to attempt to classify processes comparably across levels.
A formal identity among concrete systems is demonstrated by a procedure composed of three logically independent steps: (a) recognizing an aspect of two or more systems which has comparable status in those systems, (b) hypothesizing a quantitative identity between them, and (c) empirically demonstrating that identity within a certain range of error by collecting data on a similar aspect of each of the two or more systems being compared. Thus a set of observations at one level of living systems can be associated with findings at another, to support generalizations that are far from trivial. It may be possible to use the same conceptual system to represent two quite different sorts of concrete systems, or to make models of them with the same mathematical constructs. It may even be possible to formulate useful generalizations which apply to all living systems at all levels. A comparison of systems is complete only when statements of their formal identities are associated with specific statements of their interlevel, intertype, and interindividual disidentities. The confirmation of formal identities and disidentities is done by empirical study.
In order to make it easier to recognize similarities that exist in systems of different types and levels, it is helpful to use general systems terms. These words are carefully selected according to the following criteria:
(a) They should be as acceptable as possible when applied at all levels and to all types of living systems. For example, “sense organ” is one word for the subsystem that brings information into the system at the level of organisms, but “input transducer” is also satisfactory, and it is a more acceptable term for that subsystem at the society level (e.g., a diplomat, foreign correspondent, or spy) or in an electronic system. Consequently I use it. I select terms which refer to a commonality of structure or process across systems. Such a usage may irritate some specialists used to the traditional terminology of their fields. After all, one of the techniques we all use to discover whether a person is competently informed in a certain field is to determine through questioning whether he can use its specialized terminology correctly. A language which intentionally uses words that are acceptable in other fields is, of necessity, not the jargon of the specialty. Therefore whoever uses it may be suspected of not being informed about the specialty. The specialist languages, however, limit the horizons of thought to the borders of the discipline. They mask important intertype and interlevel generalities which exist and make general theory as difficult as it is to think about snow in a language that has no word for it. Since no single term can be entirely appropriate to represent a structure or process at every level, readers of general systems literature must be flexible, willing to accept a word to which they are not accustomed, so long as it is precise and accurate, if the term is useful in revealing cross-type and cross-level generalities. I do not wish to create a new vocabulary but to select, from one level, words which are broadly applicable, and to use them in a general sense at all levels. This is done recognizing that these terms have synonyms or near synonyms which are more commonly employed at certain levels. Actually, with the current usages of scientific language, it is impossible always to use general systems words rather than type-specific and level-specific words because the discussion would appear meaningless to experts in the field. In this book I use the general systems words as much as seems practicable.
(b) The terms should be as neutral as possible. Preferably they should not be associated exclusively with any type or level of system, with biological or social science, with any discipline, or with any particular school or theoretical point of view.
What are some examples of the sort of general systems terms I shall use? For a structure, “ingestor.” This is the equivalent of a number of different words used at the various levels, for example: cell-aperture in the cell membrane; organ-hilum; organism-mouth; group-the family shopper; organization-the receiving department; society-the dock workers of a country; supranational system-those dock workers of nations in an alliance who are under unified command. For a process, “moving.” This is a close equivalent of: cell-contraction; organ-peristalsis; organism-walking; group-hiking; organization-moving a factory; society-nomadic wandering; supranational system-migration (but it is questionable whether any supranational system has ever done this).
8.2 Intersystem differentiation
All systems at each level have certain common and distinct characteristics which differentiate them from systems at other levels. There are regular differences across levels, from lowest to highest, for several variables of structure and process. Although the ranges of these variations at two or more levels may overlap, the average is ordinarily distinctive for each level. These variables include average size (cells are small, supranational systems large); average duration as a system; amount of mobility of units in physical space; degree of spatial cohesiveness among units over time; density of distribution of units; number of distinguishable processes; complexity of processes; transferability of processes from one component to another; and rate of growth. The striking cross-level differences in mobility of system units are among the chief reasons why many scientists have difficulty in recognizing the fundamental similarity of the living systems studied by biologists and those studied by social scientists. Systems at the organism level, for instance, have components with much less mobility in relation to one another, more fixed spatial relationships, and more readily observable boundaries than groups, whose members often move about rapidly and easily disperse to reunite at a later time. A given process is usually carried out by the same component in organisms; in groups it is often transferred from one member to another.
Within each level, systems display type differences and individual differences. No two specific organisms – two lions or two dandelions – are exactly alike. No two groups – two teams or two families – have exactly identical compositions or interactions.
When interindividual, intertype, and interlevel formal identities among systems are demonstrated, they are of absorbing scientific interest. Very different structures carry out similar processes and also perform them similarly, so that they can be quite precisely described by the same formal model. Conversely, it may perhaps be shown as a general principle that subsystems with comparable structures, but quite different processes, may have quantitative similarities as well.
I shall discuss numerous hypotheses about cross-level formal identities concerned with either structure or process. They are the warp of general living systems theory. The woof comprises the disidentities, differences among the levels. The ultimate task in making predictions about living systems is to learn the quantitative characteristics of the general, cross-level formal identities on the one hand and the interlevel, intertype, and interindividual differences on the other, combining both in a specific prediction. One example of this sort of formal identity which I have studied in detail is the response of systems at five levels to “information input overload.”
8.3 Emergents.
I have stated that a measure of the sum of a system’s units is larger than the sum of that measure of its units. Because of this, the more complex systems at higher levels manifest characteristics, more than the sum of the characteristics of the units, not observed at lower levels. These characteristics have been called emergents. Significant aspects of living systems at higher levels will be neglected if they are described only in terms and dimensions used for their lower-level subsystems and components.
It is the view of Braynes, Napalkov, and Svechinskiy that the remarkable capabilities of both the computer and the human brain derive from the complex way in which the elements are combined. Individual nerve cells, and parts of the computer, have less functional scope. I agree that certain original aspects – new patterns of structure and process – are found at higher levels which are not seen at lower ones. For these new qualities new terms and dimensions are needed. But that is no reason for a complete, new conceptual system. Scientific unity and parsimony are advanced if we simply add the necessary new concepts to those used at lower levels. Moreover, it is vital to be precise in describing emergents. Many have discussed them in vague and mystical terms. I oppose any conceptualization of emergents (like that held early, and later rejected, by some Gestalt psychologists) that involves inscrutable characteristics of the whole, greater than the sum of the parts, which are not susceptible to the ordinary methods of scientific analysis.
A clear-cut illustration of emergents can be found in a comparison of three electronic systems. One of these – a wire connecting the poles of a battery – can only conduct electricity, which heats the wire. Add several tubes, condensers, resistors, and controls, and the new system can become a radio, capable of receiving sound messages. Add dozens of other components, including a picture tube and several more controls, and the system becomes a television set, which can receive sound and a picture. And this is not just more of the same. The third system has emergent capabilities the second system did not have, emergent from its special design of much greater complexity, just as the second has capabilities the first lacked. But there is nothing mystical about the colored merry-go-round and racing children on the TV screen – it is the output of a system which can be completely explained by a complicated set of differential equations such as electrical engineers write, including terms representing the characteristics of each of the set’s components.
Shred-out – the adoption by living systems at higher levels of newer, more complex ways of carrying out fundamental processes – may explain the evolutionary rise of emergent characteristics. Butler discusses these concepts, giving examples from the level of the atom on up, as follows:
We may be able to break down the organism into its cells, and the cells into the interlocking component cycles of activity, yet the functioning cell is more than the sum of the chemical processes of which it is made up and the organism is more than the sum of the cells of which it is composed.
This can be illustrated by a simple example. If we combine a number of atoms of carbon, hydrogen, nitrogen, and oxygen together in a particular way, we obtain the vivid blue dye, methylene blue. We could not have suspected from what we knew of these atoms that, when combined in this way, they would exhibit this property. Nevertheless, once we have the dye, we may be able to account for its properties in terms of the atoms and their mode of combination. We can, for example, account for the colour as due to the oscillation of electrons in a particular cyclic molecular framework, and this can be ‘explained’ in terms of the electronic structure of the atoms themselves. If necessary we may and we frequently must add to our description of the atoms in order to enable us to account for methylene blue and other substances in terms of them, but we could hardly have predicted methylene blue (or other dyes) if we were completely ignorant of its existence and behaviour. . . .
In just the same way we see new kinds of behaviour emerging at the different levels of life, which could hardly have been predicted if only the simpler systems which are made use of were known.
The new level of organisation can be analysed into its component mechanisms, and the new organisation is implicit in the components, but nevertheless when it has been achieved, something new has appeared, which is more than the sum of the separate mechanisms of which it is made up. From this point of view, we see, as Bergson did in his concept of emergent evolution, that in the course of evolution there has not only been an increase of complexity of the parts, but also the emergence of new properties, which although they are potentially present in the simpler systems, do not really exist until they are actually produced and when they are achieved are essentially more than the isolated parts.
9. Echelon
This concept may seem superficially similar to the concept of level, but it is distinctly different. Many complex living systems, at various levels, are organized into two or more echelons. (I use the term in the military sense of a step in the “chain of command,” not in the other military sense of arrangement of troops in rows in physical space.) In living systems with echelons the components of the decider, an information processing subsystem, are hierarchically arranged. Certain types of decisions are made by one component of that subsystem and others by another, each component being at a different echelon. All echelons are within the boundary of the decider subsystem. Ordinarily each echelon is made up of components of the same level as those which make up every other echelon in that system. Characteristically the decider component at one echelon gets information from a source or sources which process information primarily or exclusively to and from that echelon. At some levels of living systems – e.g., groups – the decider is often not organized in echelon structure.
After a decision is made at one echelon on the basis of the information received, it is transmitted, often, through a single subcomponent (which may or may not be the same as the decider) but possibly through more than one subcomponent, upward to the next higher echelon, which goes through a similar process, and so on to the top echelon. Here a final decision is made, and then command information is transmitted downward to lower echelons. Characteristically information is abstracted or made more general as it proceeds upward from echelon to echelon, and it is made more specific or detailed as it proceeds downward. If a component does not decide but only passes on information, it is not functioning as an echelon. In some cases of decentralized decision making, certain types of decisions are made at lower echelons and not transmitted to higher echelons in any form, while information relevant to other types of decisions is transmitted upward. If there are multiple parallel deciders, without a hierarchy that has subordinate and superordinate deciders, there is not one system but multiple ones.
10. Suprasystem
10.1 Suprasystem and environment.
The suprasystem of any living system is the next higher system in which it is a component or subsystem. For example, the suprasystem of a cell or tissue is the organ it is in; the suprasystem of an organism is the group it is in at the time. Presumably every system has a suprasystem except the “universe.” The suprasystem is differentiated from the environment. The immediate environment is the suprasystem minus the system itself. The entire environment includes this plus the suprasystem and the systems at all higher levels which contain it. In order to survive, the system must interact with and adjust to its environment, the other parts of the suprasystem. These processes alter both the system and its environment. It is not surprising that characteristically living systems adapt to the environment and, in return, mold it. The result is that, after some period of interaction, each in some sense becomes a mirror of the other. For example, Emerson has shown how a termite nest, an artifact of the termites as well as part of their environment, reveals to inspection by the naturalist, long after the termites have died, much detail about the social structure and function of those insects. Likewise a pueblo yields to the anthropologist facts about the life of the Indians who inhabited it centuries ago. Conversely, living systems are shaped by their environment. Sailors’ skins are weathered and cowboys’ legs are bowed. As Tolman pointed out, each of us carries with him a “cognitive map” of the organization of his environment, of greater or lesser accuracy – stored information, memories, which are essential for effective life in that environment.
10.2 Territory.
The region of physical space occupied by a living system, and frequently protected by it from an invader, is its territory. Examples are a bowerbird’s stage, a dog’s yard, a family’s property, a nation’s land. The borders of the territory are established conceptually and stored by the occupants as information, a more or less precise cognitive map in the memory, being conveyed by signals to neighboring living systems (sometimes including scientific observers) which also store a similar cognitive map in their memories. Neighboring living systems may not have identical maps stored in their memories, which can lead to conflict among them. The border of the territory must be distinguished from the boundary of the living system occupying it, the boundary being made up of living components and sometimes also artifacts. The boundary may be coextensive with the edges of the territory, but often it covers a smaller region, and it may move over the edges of its system’s territory into others surrounding it.
11. Subsystem and component
In every system it is possible to identify one sort of unit, each of which carries out a distinct and separate process, and another sort of unit, each of which is a discrete, separate structure. The totality of all the structures in a system which carry out a particular process is a subsystem. A subsystem, thus, is identified by the process it carries out. It exists in one or more identifiable structural units of the system. These specific, local, distinguishable structural units are called components or members or parts. I have referred to these components in my definition of a concrete system as “a nonrandom accumulation of matter-energy, in a region in physical space-time, which is organized into interacting, interrelated subsystems or components.” There is no one-to-one relationship between process and structure. One or more processes may be carried out by two or more components. Every system is a component, but not necessarily a subsystem of its suprasystem. Every component that has its own decider is a system at the next lower level, but many subsystems are not systems at the next lower level, being dispersed to several components.
The concept of component process is related to the concept of role used in social science. Organization theory usually emphasizes the functional requirements of the system which the component fulfills, rather than the specific characteristics of the component or components that make up the subsystem. The typical view is that an organization specifies clearly defined roles (or component processes) and human beings “fill them.” But it is a mistake not to recognize that characteristics of the component – in this case the person carrying out the role – also influence what occurs. A role is more than simple “social position,” a position in some social space which is “occupied.” It involves interaction, adjustments between the component and the system. It is a multiple concept, referring to the demands upon the component by the system, to the internal adjustment processes of the component, and to how the component functions in meeting the system’s requirements. The adjustments it makes are frequently compromises between the requirements of the component and the requirements of the system.
It is conceivable that some systems might have no subsystems or components, although this would be true only of an ultimate particle. The components of living systems need not be alive. Cells, for example, are composed of nonliving molecules or complexes of molecules. Systems of less than a certain degree of complexity cannot have the characteristics of life.
Often the distinction between process units and structural units, between subsystems and components, is not clearly recognized by scientists. This results in confusion. For example, when most physiologists use the word “organ” they refer to a process unit, while most anatomists use the term to refer to a structural unit. Yet the same word is used for both.
Sometimes confusion is avoided by giving a unit of a system both a structural name and a title referring to the process or role it carries out. Elizabeth Windsor is a structural name and her process title is Queen.
It is notoriously hard to deduce process from structure, and the reverse is by no means easy. Thomas Wharton, the seventeenth-century anatomist, demonstrated how delightfully wrong one can be in determining a subsystem’s process from its structure. After carefully examining the thyroid gland, he concluded that it had four purposes: (a) to serve as a transfer point for the superfluous moisture from the nerves through the lymphatic ducts to the veins which run through the gland; (b) to keep the neck warm; (c) to lubricate the larynx, so making the voice lighter, more melodious, and sweeter; and (d) to round out and ornament the curve of the neck, especially in women.
Such confusion about the process carried out by a structure can exist at any level: a lively argument still persists as to whether during President Woodrow Wilson’s illness he was the nation’s chief executive and decision maker, or whether it was his wife or his physician, Dr. Cary T. Grayson. Everyone who has ever served on a committee knows that Cohen may be the chairman, but Kelly can be the leader, or vice versa.
In defining “system” I indicated that the state of its units is constrained by, conditioned by, or dependent upon the state of other units. That is, the units are coupled. Some systems and components are also constrained by their suprasystems and subsystems. The form of allocation of process to structure determines the nature of the constraint or dependency in any given system. Living systems are so organized that each subsystem and component has some autonomy and some subordination or constraint from lower-level systems, other systems at the same level, and higher-level systems. Conflicts among them are resolved by adjustment processes.
The way living systems develop does not always result in a neat distribution of exactly one subsystem to each component. The natural arrangement would appear to be for a system to depend on one structure for one process, but such a one-to-one relationship does not always exist. Sometimes the boundaries of a subsystem and a component exactly overlap; they are congruent. Sometimes they are not congruent. Other possibilities include: (a) a single subsystem in a single component, (b) multiple subsystems in a single component, (c) a single subsystem in multiple components, or (d) multiple subsystems in multiple components.
Systems differ markedly from level to level, type to type, and perhaps somewhat even from individual to individual, in their patterns of allocation of various subsystem processes to different structures. Such process may be (a) localized in a single component, (b) combined with others in a single component, (c) laterally dispersed to other components in the system, (d) upwardly dispersed to the suprasystem or above, (e) downwardly dispersed to subsystems or below, or (f) outwardly dispersed to other systems external to the hierarchy it is in. Which allocation pattern is employed is a fundamental aspect of any given system. For a specific subsystem function in a specific system one strategy results in more efficient process than another. One can be better than another in maximizing effectiveness and minimizing costs. Valuable studies can be made at every level on optimal patterns of allocation of processes to structures. In all probability some general systems principles must be relevant to such matters. Possible examples are: Structures which minimize the distance over which matter-energy must be transported or information transmitted are the most efficient. If multiple components carry out a process, the process is more difficult to control and less efficient than if a single component does it. If one or more components which carry out a process are outside the system, the process is more difficult to integrate than if they are all in the system. Or if there are duplicate components capable of performing the same process, the system is less vulnerable to stress and therefore is more likely to survive longer, because if one component is inactivated, the other can carry out the process alone.
In this book I shall emphasize cross-level and cross-type formal identities among similar subsystems (units which carry out comparable processes) rather than among components (units which may look alike but which carry out unlike processes). The history of the life sciences suggests that it is more profitable to generalize about similar subsystems than about similar components. Generalizing about similar subsystems, therefore, is a central principle of the research strategy outlined in succeeding chapters.
The following sorts of subsystems and other contents exist in living systems or are associated with them:
11.1 Local subsystem.
If the boundary of a subsystem is congruent with the boundary of a component, and all its parts are contiguous in space, it is a local subsystem, limited to one component. The system in this case is dependent on only one component for the process.
11.2 Combined subsystem.
If the boundary of a subsystem is not congruent with the boundary of a component, and the subsystem is located in a smaller region than the component, sharing the region with one or more other subsystems, it is a combined subsystem. The system in this case is dependent on part of one component for the process.
11.3 Laterally dispersed subsystem.
If the boundary of a subsystem is not congruent with the boundary of a component, and the subsystem is located in a larger region, including more than one component of the system, it is a laterally dispersed subsystem. In this case the system is dependent on multiple components for the process. To coordinate these components there must be a sufficient degree of communication among the parts so that they are able to interact.
11.4 Joint subsystem.
At times a subsystem may be simultaneously a part of more than one local concrete system – for example, when one person plays the fourth position at two bridge tables or when a yeast cell is budding into two. A joint subsystem usually interacts with only one system at a given level at anyone moment, though its relationships fluctuate rapidly. In this case the system is dependent for the process on a component it shares with another system.
11.5 Upwardly dispersed subsystem.
If the subsystem boundary is not congruent with a component boundary, but the process is carried out by a system at a higher level, it is an upwardly dispersed subsystem. In this case the system is dependent on a suprasystem for the process.
11.6 Downwardly dispersed subsystem.
If the subsystem is not congruent with any component, but the process is carried out by a subsubsystem at a lower level, it is a downwardly dispersed subsystem. In this case the system is dependent on a subsubsystem for the process.
11.7 Outwardly dispersed subsystem.
If the boundary of a subsystem is not congruent with the boundary of a component, but the process is carried out by another system, living or not, it is an outwardly dispersed subsystem. If the other system performs the process in exchange for nothing or at its own expense, parasitism exists. If it carries out the process in exchange or economic trade-off for some reward or service which constitutes a cost to the first system, symbiosis exists. In either case the system is dependent for the process upon another system, at the same or at another level. By definition we shall not call it parasitism or symbiosis if the dependence is on the system’s suprasystern or systems at higher levels which include it, or on a subsubsystem or systems at lower levels included in it. A person may be parasitically or symbiotically dependent on cells of another person (e.g., blood transfusion recipients) or on organs of another (e.g., kidney transplant recipients) or on another organism (e.g., a blind man with a leader dog) or on another group than his own family (e.g., the “Man Who Came to Dinner”) or on another organization than his own (e.g., a visiting professor) or on another nation (e.g., a foreign tourist). Such assistance is required for all partipotential systems and all totipotential ones which are not functioning fully. If they did not have this aid they would not survive.
When a member of a family goes away to college he ceases to be a subsystem of the local concrete family group and becomes parasitic or symbiotic on the college organization. He may keep in sufficient touch through the use of the telephone or by mail to coordinate his plans with the family and play a part in its interactions. The family may spend a large part of its existence in dispersed form, coming together only for reunions. The group can be coordinated by information flows so that all members convene at the same time. If the information flows break down, the group may cease to exist. Foreign secret agents who are dispersed into social systems are sometimes detected because their secret radio messages or other information transmissions are monitored and their participation in another system discovered. The coordination and mutual influence require information flow, and the agent must communicate if he is to follow the directives of his government and also send back intelligence to it.
11.8 Critical subsystem.
Certain processes are necessary for life and must be carried out by all living systems that survive or be performed for them by some other system. They are carried out by the following critical subsystems: reproducer, boundary, ingestor, distributor, converter, producer, matter-energy storage, extruder, motor, supporter, input transducer, internal transducer, channel and net, decoder, associator, memory, decider, encoder, and output transducer. Of these, only the decider is essential, in the sense that a system cannot be parasitic upon or symbiotic with another system for its deciding. A living system does not exist independently if its decider is dispersed upwardly, downwardly, or outwardly.
Since all living systems are genetically related, have similar constituents, live in closely comparable environments, and process matter-energy and information, it is not surprising that they should have comparable subsystems and relationships among them. All systems do not have all possible kinds of subsystems. They differ individually, among types and across levels, as to which subsystems they have and how those subsystems are structured. But all living systems either have a complement of the critical subsystems carrying out the functions essential to life or are intimately associated with and effectively interacting with systems which carry out the missing life functions for them. Fungi and plants may lack a motor and some information processing subsystems.
Often there are structural cues as to which are the critical subsystems. Natural selection has wiped out those species whose critical subsystems were vulnerable to stresses in the environment. Those have survived whose critical subsystems are either duplicated (like the kidney) or especially well protected (like the brain suspended in fluid in a hard skull or the embryo suspended in amniotic fluid in the uterus). So structural characteristics may reveal the secrets of process.
11.9 Inclusion.
Sometimes a part of the environment is surrounded by a system and totally included within its boundary. Any such thing which is not a part of the system’s own living structure is an inclusion. Any living system at any level may include living or nonliving components. The amoeba, for example, ingests both inorganic and organic matter and may retain particles of iron or dye in its cytoplasm for many hours. A surgeon may replace an arteriosclerotic aorta with a plastic one and that patient may live comfortably with it for years. To the two-member group of one dog and one cat an important plant component is often added – one tree. An airline firm may have as an integral component a computerized mechanical system for making reservations which extends into all its offices. A nation includes many sorts of vegetables, minerals, buildings, and machines, as well as its land.
The inclusion is a component or subsystem of the system if it carries out or helps in carrying out a critical process of the system; otherwise it is part of the environment. Either way, in order to survive, the system must adjust to its characteristics. If it is harmless or inert it can often be left undisturbed. But if it is potentially harmful – like a pathogenic bacterium in a dog or a Greek in the giant gift horse within the gates of Troy – it must be rendered harmless or walled off or extruded from the system or killed. Because it moves with the system in a way the rest of the environment does not, it constitutes a special problem. Being inside the system, it may be a more serious or more immediate stress than it would be outside the system’s protective boundary. But also, the system that surrounds it can control its physical actions and all routes of access to it. For this reason international law has developed the concept of extraterritoriality to provide freedom of action to ambassadors and embassies, nations’ inclusions within foreign countries.
An employee, an officer, or a stockholder of a company is certainly a component in that system. But what about a client who enters the company’s store in order to buy or a customer who goes into a theater in order to see a movie? If a shopper simply wanders into a store, looks at a television set on display, and then wanders out, he was probably just an inclusion. But if a significant interaction occurs or a contract, implicit or explicit, is agreed to (as when a customer buys a ticket to enter the theater or hires a lawyer to represent him), the customer or client is an inclusion (not a component) and he is at the same time another system in the environment of the organization or firm, interacting with it in the suprasystem.
11.10 Artifact.
An artifact is an inclusion in some system, made by animals or man. Spider webs, bird nests, beaver dams, houses, books, machines, music, paintings, and language are artifacts. They may or may not be prostheses – inventions which carry out some critical process essential to a living system. An artificial pacemaker for a human heart is an example of an artifact which can replace a pathological process with a healthy one. Insulin and thyroxine are replacement drugs which are human artifacts. Chemical, mechanical, or electronic artifacts have been constructed which carry out some functions of all levels of living systems.
Living systems create and live among their artifacts. Beginning presumably with the hut and the arrowhead, the pot and the vase, the plow and the wheel, mankind has constructed tools and devised machines. The industrial revolution of the nineteenth century, capped by the recent harnessing of atomic energy, represents the extension of man’s matter-energy processing ability, his muscles. A new industrial revolution, of even greater potential, is just beginning in the twentieth century, with the development of information and logic processing machines – adjuncts to man’s brain. These artifacts are increasingly becoming prostheses, relied on to carry out critical subsystem processes. A chimpanzee may extend his reach with a stick; a man may extend his cognitive skills with a computer. Today’s prostheses include input transducers which sense the type of blood cells that pass before them and identify missiles that approach a nation’s shores; photographic, mechanical, and electronic memories which can store masses of information over time; computers which can solve problems, carry out logical and mathematical calculations, make decisions, and control other machines; electric typewriters, high-speed printers, cathode-ray tubes, and photographic equipment which can output information. An analysis of many modem system must take into account the novel problems which arise at man-machine interfaces.
Music is a special sort of human artifact, an information processing artifact. So are the other arts and cognitive systems which people share. So is language. Whether it be a natural language or the machine language of some computer system, it is essential to information processing. Often stored only in human brains and expressed only by human lips, language can also be recorded on nonliving artifacts like stones, books, and magnetic tapes. It is not of itself a concrete system. It changes only when man changes it. As long as it is used, it is in flux, because it must remain compatible with the ever-changing living systems that use it. But the change emanates from the users, and without their impact the language is inert. The artifactual language used in any information transmission in a system determines many essential aspects of that system’s structure and process. Scientists sometimes neglect to distinguish between living systems and their artifacts. Because artifacts are the products of living systems, they often mirror aspects of their producers and thus have systems characteristics of their own. Termites’ nests, pots and jewelry of primitive tribes, and modern buildings are all concrete systems which can be studied for themselves alone as well as to understand the living systems that produced them. But they themselves are not living systems. Systems theory can also be applied to the history, dynamics over time, rules of change, and other aspects of languages or music, if they are viewed as abstracted systems independent of the living systems that produced or used them. This may be desirable because their producers or users may be long dead or unavailable for study.
12. Transmissions in concrete systems
All process involves some sort of transmission among subsystems within a system, or among systems. There are inputs across the boundary into a system, internal processes within it, and outputs from it. Each of these sorts of transmissions may consist of either (a) some particular form of matter; (b) energy, in the form of light, radiant energy, heat, or chemical energy; or (c) some particular pattern of information. The terms “input” and “output” seem preferable to “stimulus” and “response,” which are used in some of the behavioral sciences, because the former terms make it easy to distinguish whether the transmission is of matter, energy, or information, whereas the latter terms often conceal this distinction.
The template, genetic input or charter, of a system is the original information input that is the program for its later structure and process, which can be modified by later matter-energy or information inputs from its environment. This program was called an “instruction” by von Neumann.
13. Steady state
When opposing variables in a system are in balance, that system is in equilibrium with regard to them. The equilibrium may be static and unchanging or it may be maintained in the midst of dynamic change. Since living systems are open systems, with continually altering fluxes of matter-energy and information, many of their equilibria are dynamic and are often referred to as flux equilibria or steady states. These may be unstable, in which a slight disturbance elicits progressive change from the equilibrium state – like a ball standing on an inverted bowl; or stable, in which a slight disturbance is counteracted so as to restore the previous state – like a ball in a cup; or neutral, in which a slight disturbance makes a change but without cumulative effects of any sort – like a ball on a flat surface with friction.
All living systems tend to maintain steady states (or homeostasis) of many variables, keeping an orderly balance among subsystems which process matter-energy or information. Not only are subsystems usually kept in equilibrium, but systems also ordinarily maintain steady states with their environments and suprasystems, which have outputs to the systems and inputs from them. This prevents variations in the environment from destroying systems. The variables of living systems are constantly fluctuating, however. A moderate change in one variable may produce greater or lesser alterations in other related ones. These alterations may or may not be reversible.
13.1 Stress, strain, and threat.
There is a range of stability for each of numerous variables in all living systems. It is that range within which the rate of correction of deviations is minimal or zero, and beyond which correction occurs. An input or output of either matter-energy or information which, by lack or excess of some characteristic, forces the variables beyond the range of stability, constitutes stress and produces a strain (or strains) within the system. Input lack and output excess both produce the same strain – diminished amounts in the system. Input excess and output lack both produce the opposite strain – increased amounts. Strains may or may not be capable of being reduced, depending upon their intensity and the resources of the system. The totality of the strains within a system resulting from its template program and from variations in the inputs from its environment can be referred to as its values. The relative urgency of reducing each of these specific strains represents its hierarchy of values.
Stress may be anticipated. Information that a stress is imminent constitutes a threat to the system. A threat can create a strain. Recognition of the meaning of the information of such a threat must be based on previously stored (usually learned) information about such situations. A pattern of input information is a threat when – like the odor of the hunter on the wind, or a change in the acidity of fluids around a cell, or a whirling cloud approaching the city – it is capable of eliciting processes which can counteract the stress it presages. Processes – actions or communications – occur in systems only when a stress or a threat has created a strain which pushes a variable beyond its range of stability. A system is a constantly changing cameo, and its environment is a similarly changing intaglio, and the two at all times fit each other. That is, outside stresses or threats are mirrored by inside strains. Matter-energy storage and memory also mirror the past environment, but with certain alterations.
13.1.1 Lack stress. Ordinarily there is a standard range of rates at which each sort of input enters a system. If the input rate falls below this range, it constitutes a lack stress.
13.1.2 Excess stress. If the input rate goes above this range, it is an excess stress.
13.1.3 Matter-energy stress. Systems undergo stress in various ways. One class of stresses is the matter-energy stresses, including: (a) matter-energy input lack or underload – starvation or inadequate fuel input; (b) matter-energy input excess or overload; and (c) restraint of the system, binding it physically. (Alternative c may be the equivalent of a or b.)
13.1.4 Information stress. Systems also undergo information stresses, including: (a) information input lack or underload, resulting from a dearth of information in the environment or from improper function of the external sense organs or input transducers; (b) injection of noise into the system, which has an effect of information cutoff, much like the previous stress; and (c) information input excess or overload. Informational stresses may involve changes in the rate of information input or in its meaning.
13.1.5 The Le Châtelier principle in closed and open systems. Le Châtelier stated his principle (1888), which applies to nonliving systems and possibly also to living systems, as follows:
“Every system in chemical equilibrium undergoes, upon the variation of one of the factors of the equilibrium, a transformation in such a direction that, if it had produced itself, would have led to a variation of opposite sign to the factor under consideration.” A common restatement of this principle is: “A stable system under stress will move in that direction which tends to minimize the stress.” That is, a compensatory force will develop which will tend to minimize the effect of stress; it will be exerted opposite to the stress, and it is usually accompanied by changes in other related, subsidiary variables. By this we mean system variables not primarily and directly affected by the applied stress.
This principle or theorem was originally stated after a consideration of the thermodynamics of closed systems, but it has been adapted for open systems by Prigogine. Furthermore, a related theorem has been developed by Prigogine concerning steady states in open systems. He has stated that, for a fairly general class of cases, such steady states approach minimum entropy production. It is possible for entropy not to increase in such systems, and they are able to maintain steady states. Figure 2-3 represents one possible model for such a system in steady state. If a ping-pong ball is held in a kitchen strainer,
it is possible to blow horizontally through a straw at the ball. The faster the stream of air moves, the higher the ball rises in the strainer, until finally it passes a critical point and goes over the edge. Then a change of state results.
Vertical downward forces (G) tend to return the ball as close as possible to the equilibrium point. Something is minimized in such systems, and it appears to be the rate of change of entropy production. The single variable (V) which, according to Le Châtelier’s principle, tends to return the ball as close as possible to the equilibrium point, is equal and opposite in effect to the stream of air coming in. Within the system this variable or equilibratory force tends to operate at the expense of certain other associated variables related to adjustment processes of the system. There are, of course, fluctuations in these variables over time. Systems which maintain stability over long periods of time apparently tend to reduce the costs involved in the activation of these associate variables.
13.2 Adjustment processes. Those processes of subsystems which maintain steady states in systems, keeping variables within their ranges of stability despite stresses, are adjustment processes. In some systems a single variable may be influenced by multiple adjustment processes. As Ashby has pointed out, a living system’s adjustment processes are so coupled that the system is ultrastable. This characteristic can be illustrated by the example of an army cot. It is made of wires, each of which would break under a 120-kg weight, yet it can easily support a sleeper of that weight. The weight is applied to certain wires, and as it becomes greater, first nearby links and then those farther and farther away, take up part of the load. Thus a heavy weight which would break any of the component wires alone can be sustained. In a living system, if one component cannot handle a stress, more and more others are recruited to help. Eventually the entire capacity of the system may be involved in coping with the situation.
13.2.1 Feedback. The term feedback means that two channels exist, carrying information, such that channel B loops back from the output to the input of channel A and transmits some portion of the signals emitted by channel A (see Fig. 2-4.) These are tell-tales
or monitors of the outputs of channel A. The transmitter on channel A is a device with two inputs, formally represented by a function with two independent variables, one the signal to be transmitted on channel A and the other a previously transmitted signal fed back on channel B. The new signal transmitted on channel A is selected to decrease the strain resulting from any error or deviation in the feedback signal from a criterion or comparison reference signal indicating the state of the output of channel A which the system seeks to maintain steady. This provides control of the output of channel A on the basis of actual rather than expected performance.
The feedback signals have a certain probability of error. They differ in the lag in time which they require to affect the system. Their lag may be minimal, so that each one is fed back to the input of the latter channel before the next signal is transmitted. Or their lag may be longer and several signals may be transmitted before they arrive to affect the decision about what signal to transmit next. Feedback signals also differ in their gain or extent of corrective effect. When the signals are fed back over the feedback channel in such a manner that they increase the deviation of the output from a steady state, positive feedback exists. When the signals are reversed, so that they decrease the deviation of the output from a steady state, it is negative feedback. Positive feedback alters variables and destroys their steady states. Thus it can initiate system changes. Unless limited, it can alter variables enough to destroy systems. Negative feedback maintains steady states in systems. It cancels an initial deviation or error in performance. As Ashby says: “the importance of feedback as a necessary method for the correction of error is now accepted everywhere.”
Cybernetics, the study of methods of feedback control, is an important part of systems theory. It has led to the recognition of certain formal identities among various sorts of nonliving and living systems. In a complex system, control is achieved by many finely adjusted, interlocking processes involving transmissions of matter-energy and information.
There are many such systems, living and nonliving. An automatic tracking device is one nonliving example. By means of such a device, aircraft-to-aircraft fire-control systems may be set up that keep guns or missiles pointed accurately at a maneuvering target in spite of the motion of the plane in which they are mounted.
Steady states in all living systems are controlled by negative feedbacks. A living system is self-regulating because in it input not only affects output, but output often adjusts input. The result is that the system adapts homeostatically to its environment. Elkinton and Danowski point out how complex these physiological self-regulating servomechanisms of mammalian organisms are. They illustrate this by the example of bodily water balance:
The output of water in excess of electrolyte controlled by the antidiuretic hormone in the kidney, produces a rise in extra-cellular electrolyte concentration. The rise in this concentration feeds back to the osmoreceptors in the hypothalamus to stimulate the production of antidiuretic hormone (ADH) in the supraoptico-hypophyseal system, and so the error in output of water tends to be corrected. At the same time this system is linked to regulation of intake through thirst. Hypertonicity of extra-cellular fluid with resultant cellular dehydration stimulates thirst and increased intake of water as well as the production of ADH. Thus both intake and output are regulated to minimize error in water content of the body.
They go on to describe the further relationships of sodium, appetite, and water balance:
It is tempting to consider the possibility of describing all these linked servomechanisms in the organism in terms of control of energy exchange with the environment. Thus the total body content of solids and fluids is maintained in the healthy adult at a constant level with oscillation about a mean. . . . The dynamics of the body fluids are one aspect of the integrated function of the organism by which a steady state is maintained with the aid of exogenous energy ultimately derived from the sun.
Vickers describes adjustment processes of living systems in terms of feedbacks which correct deviations of systems from desirable states, as follows:
The problem for R [a regulating process] is to choose a way of behaving which will neutralize the disturbance threatening the maintenance of E [a desirable state]. Success means initiating behavior which will reduce the deviation between the actual course of affairs and the course which would be consonant with E; or at least preventing its nearer approach to the limit of the unacceptable or the disastrous.
This decision is a choice between a limited number of alternatives. Men and societies have only a finite number of ways of behaving, perhaps a much smaller number than we realize; and the number actually available and relevant to a given situation is far smaller still. It is thus essential to regard these decisions as the exercise of restricted choice.
These decisions are of four possible kinds. When the usual responses fail, the system may alter itself, for instance by learning new skills or reorganizing itself so as to make new behaviors possible; it may alter the environment; it may withdraw from the environment and seek a more favorable one; or it may alter E [a desirable state]. These are possible, if at all, only within limits; and all together may prove insufficient.
It remains to ask how men and societies choose from among these alternatives, when choose they must. In brief, the answer is “by experience.”
At every level of living systems numerous variables are kept in a steady state, within a range of stability, by negative feedback controls. When these fail, the structure and process of the system alter markedly – perhaps to the extent that the system does not survive. Feedback control always exhibits some oscillation and always has some lag. When the organism maintains its balance in space, this lag is caused by the slowness of transmissions in the nervous system but is only of the order of hundredths of a second. An organization like a corporation may take hours to correct a breakdown in an assembly line and days or weeks to correct a bad management decision. In a society the lag can sometimes be so great that, in effect, it comes too late. General staffs often plan for the last war rather than the next. Governments receive rather slow official feedbacks from the society at periodic elections. They can, however, get faster feedbacks from the press, other mass media, picketers, or demonstrators. Public opinion surveys can accelerate the social feedback process. The speed and accuracy of feedback have much to do with the effectiveness of the adjustment processes they mobilize.
There are various different types of feedback:
13.2.1.1 Internal feedback. Such a feedback loop never passes outside the boundary of the system. An example is the temperature-control mechanism of mammals.
13.2.1.2 External feedback. Such a loop passes outside the system boundary: for instance, when a patient asks a nurse to bring him an extra blanket for his bed.
13.2.1.3 Loose feedback. Such a loop permits marked deviations from steady state, or error, before initiating corrections. In a democratic country, for instance, an elected official usually remains in office for his entire term even though his constituency disapproves of his actions.
13.2.1.4 Tight feedback. Such a loop rapidly corrects any errors or deviations. An illustration is a tightrope-walker’s balance control.
From a study of electronic systems which carry out some sort of adaptive control, Kazda has listed five functional types of feedback. Each of these types, and combinations of them, can be found among the complexly adaptive living systems. They are:
13.2.1.5 Passive adaptation. Achieves adaptation not by changing system variables but by altering environmental variables. Examples: a heater controlled by a thermostat; a snake’s temperature control.
13.2.1.6 Input-signal adaptation. Adapts to changes in characteristics of the input signal by altering system variables. Examples: automatic radio volume control; iris of the eye.
13.2.1.7 Extremum adaptation. Self-adjusts for a maximum or minimum of some variable. Examples: a computer which minimizes passenger waiting time for a battery of elevators; a department store buyer who purchases as cheaply as possible articles which he thinks his store can sell for the best profit.
13.2.1.8 System-variable adaptation. Bases self-adjustment on measurement of system variables. Examples: an automatic train dispatcher; a political system which counts votes to determine policies.
13.2.1.9 System-characteristic adaptation. Self-adjustment based on measurements made on the output of the system. Examples: an autogyro; a student who practices speaking in a foreign language by listening to recordings of his own speech.
13.2.2 Power. In relation to energy processing, power is the rate at which work is performed, work being calculated as the product of a force and the distance through which it acts. The term also has another quite different meaning. In relation to information processing, power is control, the ability of one system to elicit compliance from another, at the same or a different level. A system transmits a command signal or message to a given address with a signature identifying the transmitter as a legitimate source of command information. The message is often in the imperative mode, specifying an action the receiver is expected to carry out. It elicits compliance at the lower levels because the electrical or chemical form of the signal sets off a specific reaction. At higher levels the receiving system is likely to comply because it has learned that the transmitter is capable of evoking rewards or punishments from the suprasystem, depending on how the receiver responds. Characteristically, in hierarchies of living systems, each level has a degree of autonomy and is also partially controlled by levels above and below it. None can have complete autonomy if the system is to be integrated effectively. A mutual “working agreement” thus is essential.
How is power or control exerted? A system transmits an information output, a command signal or message. Such a message has certain specific characteristics: (a) It has an address – it includes information indicating to what specific receiver system or systems it is transmitted, those which are to be influenced. If the channel on which it is transmitted does not branch, simply sending it on that channel gives the address information. If the channel branches, the address indicates the appropriate routing at branching points. (b) It has a signature – it includes information indicating which system transmitted it. If it travels on a channel that has only one transmitter, its presence on that channel gives the signature information. Simply having a form that can be uniquely produced by only one system can give the information. Or it may have specific signature symbols added to the content. (c) It contains evidence that the transmitter is a legitimate or appropriate source of command information to influence decisions of the receiver. In some systems commands of a certain sort are complied with regardless of the source. For example, thyroid cells respond to thyrotropic hormone regardless of whether it comes from the pituitary gland of that system or is an intravenous injection. Telephone information operators respond to requests for telephone numbers regardless of who makes them. In such systems the form of the command carries its own evidence of legitimacy. In other systems the message must include the title of the transmitter or other evidence of its legitimacy, along with the context of the command. (d) It is often literally in the imperative mood, styled as a command, but even when it is not couched in this form, it implies expectation of compliance. (e) The primary content of the message specifies an action the receiver is expected to carry out. It reinforces one alternative rather than others in a decision the receiver is constrained to make.
Why can such a message elicit compliance? At lower levels, because the electrical or chemical form of what is transmitted sets off a specific reaction. At higher levels, because the receiving system is part of a suprasystem that can transmit rewarding and punishing inputs to it. The receiver has learned that, because the signature indicates that the message is from a legitimate source capable of influencing some part of the suprasystem to make such inputs, there is a certain significant probability of receiving such rewards or punishments, depending on how it responds. This is why legitimacy of the source is important; it indicates that the message is from a transmitter which has an established relationship with the suprasystem and can therefore influence the receiver through it. This fact helps to determine values and purposes or goals of the system, motivating it to act in compliance with the command. Mrs. Martin, for example, can command Mrs. Wrenn’s support in the women’s club election because Mrs. Martin is on the committee which selects the girls to be invited to serve at the annual Christmas party, and Mrs. Wrenn has a daughter who wants to serve. Consequently Mrs. Martin has “fate control” over Mrs. Wrenn, being able to influence her actions. Power among nations frequently depends on the ability to make exchanges with other countries; a nation which can offer favorable trade inducements or foreign aid often gains a measure of control over others.
Measures of power are joint functions of: (a) the percentage of acts of a system which are controlled, i.e., changed from one alternative to another; (b) some measure of how critical the acts controlled are to the system; (c) the number of systems controlled; and (d) the level of systems controlled, since control of one system at a high level may influence many systems at lower levels.
Certain differences among systems influence how power is wielded. As I have noted, systems can be either local or dispersed. Transmitting commands throughout dispersed systems requires more energy than in local systems because the components are farther apart, and the markers must be dispatched over longer channels.
Systems, also, may be either cohesive or noncohesive. They are cohesive if the parts remain close enough together in space, despite any movement of the system, to make possible transmission of coordinating information along their channels. Otherwise they are noncohesive.
Systems, also, may be either integrated or segregated. If they are integrated, they are centralized, the single decider of the system exercising primary control. If they are segregated, there are multiple deciders, each controlling a subsystem or component. The more integrated a system is, the more feedbacks, commands, and information relevant to making and implementing the central decisions flow among its parts. Therefore the more integrated a system is, the more one part is likely to influence or control another. A system is more likely to be integrated if it is local rather than dispersed. Integration, of course, requires less energy in local than in dispersed systems. The degree of integration of a system is measured by a joint function of: (a) the percentage of decisions made by the system’s central decider; (b) the rate at which the system accurately processes information relevant to the central decisions, without significant lag or restriction of the range of messages; and (c) the extent to which conflict among systems and components is minimized.
13.2.3 Conflict. In branching channels or networks, commands may come to a receiver simultaneously from two or more transmitters. If these messages direct the receiver to do two or more acts which it can carry out successfully, simultaneously or successively, there is no problem. If they direct the receiver to carry out two or more actions which are incompatible – because they cannot be done simultaneously or because doing one makes it impossible later to do the other – a special sort of strain, conflict, arises. The incompatible commands may arise from two or more systems at the same level or at different levels. For example, two subsystems may demand more energy input, and the system may be unable to meet the demands. (Jean Valjean could not provide the bread to feed his whole family.) Or two systems are in competition for a desired input, but there is not enough for both. (An embryo develops with stunted legs because the blood supply to the lower part of the body is partially blocked.) Or a system makes demands which threaten the existence of its suprasystem. (The great powers demand a veto on all significant actions of the United Nations.) An effective system ordinarily resolves such conflicts by giving greater compliance to the command with higher priority in terms of its values. But it may resolve the conflict by many sorts of adjustment processes.
13.2.4 Purpose and goal. By the information input of its charter or genetic input, or by changes in behavior brought about by rewards and punishments from its suprasystem, a system develops a preferential hierarchy of values that gives rise to decision rules which determine its preference for one internal steady-state value rather than another. This is its purpose. It is the comparison value which it matches to information received by negative feedback in order to determine whether the variable is being maintained at the appropriate steady-state value. In this sense it is normative. The system then takes one alternative action rather than another because it appears most likely to maintain the steady state. When disturbed, this state is restored by the system by successive approximations, in order to relieve the strain of the disparity recognized internally between the feedback signal and the comparison signal. Any system may have multiple purposes simultaneously.
A system may also have an external goal, such as reaching a target in space, or developing a relationship with any other system in the environment. Or it may have several goals at the same time. Just as there is no question that a guided missile is zeroing in on a target, so there is no question that a rat in a maze is searching for the goal of food at its end or that the Greek people under Alexander the Great were seeking the goal of world conquest. As Ashby notes, natural selection permits only those systems to continue which have goals that enable them to survive in their particular environments. The external goal may change constantly – as when a hunter chases a moving fox, or a man searches for a wife by dating one girl after another – while the internal purpose remains the same.
It is not difficult to distinguish purposes from goals, as I use the terms: an amoeba has the purpose of maintaining adequate energy levels, and therefore it has the goal of ingesting a bacterium; a boy has the purpose of keeping his body temperature in the proper range, and so he has the goal of finding and putting on his sweater; Poland had the purpose in March 1939, of remaining uninvaded and autonomous, and so she sought the goal of a political alliance with Britain and France in order to have assistance in keeping both Germany and Russia from crossing her borders.
A system’s hierarchy of values determines its purposes as well as its goals. The question is often asked of the words “goal” and “purpose,” as it is of the word “value,” whether they are appropriately defined as whatever is actually preferred or sought by the system, or as what should be preferred or sought. I shall use it in the former sense, unless I indicate that the latter sense is being employed. When the latter meaning is used, I shall not imply that the norm as to what the goal should be is established in any absolute way, but rather that it is set by the system’s suprasystem when it originates its template, or by rewards and punishments. Ashby has said that: ” . . . there is no property of an organization that is good in any absolute sense; all are relative to some given environment, or to some given set of threats and disturbances, or to some given set of problems.” A system is adjusted to its suprasystem only if it has an internal purpose or external goal which is consistent with the norm established by the suprasystem. Since this is not always true, it is important to distinguish the two notions of the actual and the normative.
The reason it is important to a receiver whether a command signal is transmitted from a legitimate source is that, if it is legitimate, it can influence the suprasystem to make reward and punishment inputs to the receiver and so potentially can alter both its purposes and its goals.
It is necessary to distinguish two meanings of the term “purpose.” One is function or role of the system in the suprasystem, and the other, independent concept is the internally determined control process of the system which maintains one of its variables at a given steady-state value. In their early paper on cybernetics, Rosenblueth, Wiener, and Bigelow saw rudimentary purposive behavior in some nonliving systems, like a torpedo, which can “home” to a moving target. The concept of purpose has been made suspect to most scientists by teleological formulations which suggest that living systems strive for mystical ends which are not clearly formulated. These formulations are from the viewpoint of the scientific observer. On this topic, Rothstein has written:
One would not introduce the notion of purpose unless the system were only partially specified. With complete specification the ‘stimulus’ is specified, likewise the action of the regulator and ditto the response of the system. It is only when an ensemble of possible stimuli is considered and no information is available to predict a priori which of the ensemble will materialize that one is motivated to introduce the concept of purpose.
One can say the initial state causes the final state, or that the final state is the purpose of the initial state. In this form one can object that the concept of purpose has been reduced to an empty play on words. However, consider an experimenter interested in producing some particular situation. In many cases he sets up an initial configuration from which the desired situation will ensue because of the laws the system obeys. The final situation is the goal or purpose of the experimenter, which has determined his choice of initial conditions. In this sense, we can call his purpose the cause of the initial condition. For completely defined physical systems, there is thus no logical distinction between cause and purpose as either determines the other. Meaningful distinctions are only possible in terms of considerations extrinsic to the system. It now follows that physics is as incapable of finding a purpose or goal of the whole universe as it is of finding its origin or cause.
Rothstein believes that the next-to-last sentence is true of systems in general.
But if purpose is defined not in terms of the observer but in terms of specific values of internal variables which systems maintain in steady states by taking corrective actions, then the concept is scientifically useful. Reinterpreting purpose in concepts of modern physics, Sommerhoff maintains that the notion concerns a certain future event, a “focal condition” (in my terms, a goal). This focal condition, he says, is a determinant of a “directive correlation.” Such a correlation is characteristically found between processes in living systems and in their environments. Variables in them are so “geared” or interrelated that, within certain ranges, they will at a later time only bring about the focal condition. Such a situation requires that there was some prior state of affairs which gave rise jointly both to the processes in the system and to those in its environment. Feedback is one way such joint causation can be accomplished. Sommerhoff believes that this sort of process explains such phenomena of living systems as adaptation of individuals and species to their environments, coordination and regulation of internal system processes, repair of systems after trauma, and various sorts of behavior including learning, memory, and decision making. For example, one cannot distinguish between products which are put out by a system and wastes which are excreted without knowing the purpose of the system internally and its related goals in the suprasystem. This is graphically demonstrated by the following “Ballad of the Interstellar Merchants”:
Among the wild Reguleans
we trade in beer and hides
for sacks of mMomimotl leaves
and carcasses of brides.
They love ’em and they leave ’em,
once affection’s been displayed,
to the everloving merchants
of the Interstellar Trade.
Chorus: Don’t throw that bride away, friends
don’t turn that carcass loose.
What’s only junk on Regulus
is gold on Betelgeuse.
Engineers must know the purposes which a machine is to have, what steady-state values its variables are to have, before they begin to design it. This may or may not be related to some purpose or function in the suprasystem. Occasionally comics have built apparatuses with wheels, cogs, gears, pistons, and cams that merely operate, without any useful function in the suprasystem, or gadgets that function only to turn themselves off. If one is to understand a system, know what it is to optimize, or measure its efficiency (i.e., the ratio between the effectiveness of its performance and the costs involved), one must learn its expected function or purpose in the suprasystem. The charter of a group, organization, society, or supranational system describes this. Biologists, however, have a difficult time defining the functions of a cell, organ, or organism, except in terms of the survival of the system itself, or of the organism of which it is a part, or of its particular type.
Such facts as that a normal sea urchin can develop either from a complete egg or from a half egg led Driesch to embrace vitalism, the doctrine that phenomena of life cannot be explained in natural science terms. This sort of equifinality, he contended, could be explained only by some mystical vitalism. Equifinality means that a final state of any living system may be reached from different initial conditions and in different ways. But this is exactly what all cybernetic systems do, living and nonliving.
Bertalanffy has opposed Driesch’s views on the basis of an analysis of living systems as open systems. The steady states of open systems depend upon system constants more than environmental conditions, so long as the environment has a surplus of essential inputs. Within a wide range of inputs the composition of living tissue, for example, remains relatively constant. Of course – and Bertalanffy does not always make this clear – inputs outside the “normal” range may destroy the system or affect its structure and functioning. Each separate system, moreover, has its own history, different from others of its kind, and therefore any final state is affected by the various preceding genetic and environmental influences which have impinged upon the system. All organisms do not develop into perfect adulthood, and presumably each single cell may have slightly different characteristics as a result of its history. These limitations upon Bertalanffy’s principle do not destroy its importance. The obvious purposive activities of most living systems, which have seemed to many to require a vitalistic or teleological interpretation, can be explained as open-system characteristics by means of this principle. Some open physical systems also have this characteristic.
13.2.5 Costs and efficiency. All adjustment processes have their costs, in energy of nonliving or living systems, in material resources, in information (including in social systems a special form of information often conveyed on a marker of metal or paper money), or in time required for an action. Any of these may be scarce. (Time is a scarcity for mortal living systems.) Any of these is valued if it is essential for reducing strains. The costs of adjustment processes differ from one to another and from time to time. They may be immediate or delayed, short-term or long-term.
How successfully systems accomplish their purposes can be determined if those purposes are known. A system’s efficiency, then, can be determined as the ratio of the success of its performance to the costs involved. A system constantly makes economic decisions directed toward increasing its efficiency by improving performance and decreasing costs. Economic analyses of cost effectiveness are equally important in biological and social science but much more common and more sophisticated in social than in biological sciences. In social systems such analyses are frequently aided by program budgeting. This involves keeping accounts separately for each subsystem or component that carries out a distinct program. The matter-energy, information, money, and time costs of the program in such analyses are compared with various measures of the efficiency of performance of the program. How efficiently a system adjusts to its environment is determined by what strategies it employs in selecting adjustment processes and whether they satisfactorily reduce strains without being too costly. This decision process can be analyzed by a mathematical approach to economic decisions, or game theory. This is a general theory concerning the best strategies for weighing “plays” against “payoffs,” for selecting actions which will increase profits while decreasing losses, increase rewards while decreasing punishments, improve adjustments of variables to appropriate steady-state values, or attain goals while diminishing costs. Relevant information available to the decider can improve such decisions. Consequently such information is valuable. But there are costs to obtaining such information. A mathematical theory on how to calculate the value of relevant information in such decisions was developed by Hurley. This depends on such considerations as whether it is tactical (about a specific act) or strategic (about a policy for action), whether it is reliable or unreliable, overtly or secretly obtained, accurate, distorted, or erroneous.
14. Conclusions
The most general form of systems theory is a set of logical or mathematical statements about all conceptual systems. A subset of this concerns all concrete systems. A subsubset concerns the very special and very important living systems, i.e., general living systems theory.
My analysis of living systems uses concepts of thermodynamics, information theory, cybernetics, and systems engineering, as well as the classical concepts appropriate to each level. The purpose is to produce a description of living structure and process in terms of input and output, flows through systems, steady states, and feedbacks, which will clarify and unify the facts of life.
In such fundamental considerations it would be surprising if many new concepts appear, for countless good minds have worked long on these matters over many years. Indeed, new original ideas should at first be suspect, though if they withstand examination they should be welcomed. My intent is not to create a new school or art form but to discern the pattern of a mosaic which lies hidden in the cluttered, colored marble chips of today’s empirical facts. I may assert, along with Pascal,
Let no man say that I have said nothing new – the arrangement of the material is new. In playing tennis, we both use the same ball, but one of us places it better. I would just as soon be told that I have used old terms. Just as the same thoughts differently arranged form a different discourse, so the same words differently arranged form different thoughts.
The last thing one does in writing a book is to know what to put first.
